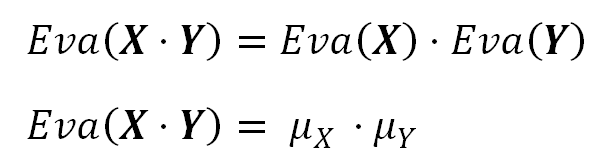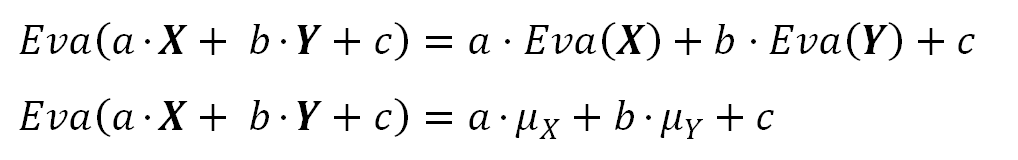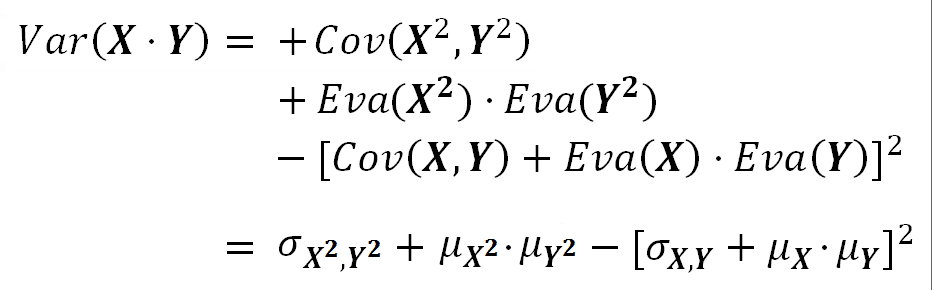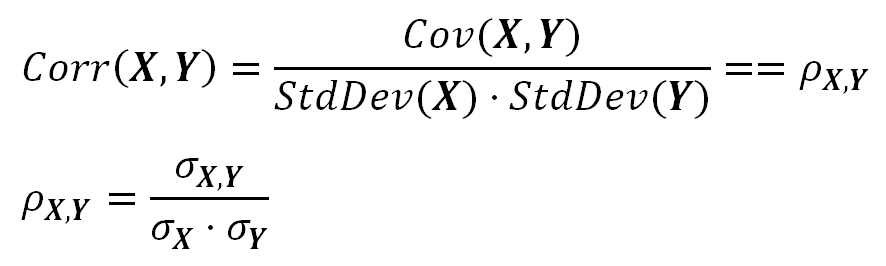This is the repository of the formulas we use along other articles. The purpose of this document is to have in a summarized way, the mathematical operators and terms along with their notation and some useful relationships between them. We won't demonstrate how to obtain them. That is out of the scope of this document and there are many resources on the web about that.
We use the "⋅" operator to denote multiplication. This way, if we see the term "abxy", in a math expression, we know it represents a single entity and not —for example— the multiplication of the terms "ab" by "xy", in which case we will use "ab⋅xy".
In these formulas, the operator "==" is used mainly to show two alternate ways to express the same thing.
Statistics Formulas
In these formulas, the symbols with bold typeface (e.g. X) represent random variables and the symbols with regular (non-bold) typeface, represent non-random variables (e.g. "c").
The Expected Value
We use the expression Eva( X ) to denote the Expected Value of the random variable X. The symbol μx represents the value resulting from that expression.
Formula 1.
Eva symbols.
The Expected Value of a non-random variable —for example a constant— is the value of that non-random variable itself:
Formula 2. Eva of a non-random variable.
The Expected Value of the product of two independent random variables is equal to the product of those variables Expected values:
Formula 3. Eva of the product of independent variables.
If the variable is scaled by a constant (a non-random variable) the Expected Value gets scaled by that constant. This is a direct consequence of the two previous formulas.
Formula 4. Eva of a scaled variable.
If two random variables are correlated, it means the value of one of them, in some degree, determines or influences the value of the other one. The Covariance is a measure of how much those variables are correlated.
For example, smoking is correlated with the probability of having cancer: the more you smoke, the greater the likelihood you eventually will get cancer.
The Expected Value of the product of two correlated random variables is equal to the product of those variables Expected values plus the Covariance of them:
Formula 5. Eva of the product of two correlated variables.
Notice how the formula 3 is a particular case of the previous formula: when the random variables are independent, the Covariance term is zero and goes away.
The Expected Value of the sum of any random variables is equal to the sum of the Expected Values of those variables. This is true regardless if those random variables are independent or not.
Formula 6. Eva of the sum of two random variables. Regardless they are independent or not.
The consolidation of the previous relationships results in the Linearity property of the Expected Value operator (Linearity of Expectation), which is true regardless the random variables are independent or not.
Formula 7. Linearity of expectation.
The Covariance
We use the expression Cov( X, Y ) to denote the Covariance of the two random variables X and Y.
Formula 8. Covariance symbols.
The Covariance is a measure of how much the values of each of two correlated random variables determines the other. If both variables change in the same way (e.g. when —in general— one grows the other also grows), the Covariance is positive, otherwise it is negative (e.g. when one increases the other decreases).
If the variables are independent the Covariance is zero. However, the Covariance must be considered zero or non zero from a statistical point of view, which means there is some fact leading us to believe the Covariance value can not be justified on the basis of chance alone.
Formula 9. Evaluation of Covariance from raw data.
If the variables are independent, their Covariance is zero. This can clearly be seen in the following formula, where if both variables were independent to each other, both terms in the subtraction become the same value and the Covariance becomes to zero:
Formula 10. Evaluation of the Covariance from the Expected values.
However, the converse of the previous rule is not alway true: If the Covariance is zero, it does not necessarily mean the random variables are independent.
For example, if X is uniformly distributed in [-1, 1], its Expected Value and the Expected Value of the odd powers (e.g. X³) of X result zero in [-1, 1]. For that reason, if the random variable Y is defined as Y = X², clearly X and Y are correlated. However, their Covariance is numerically equal to zero:
Formula 11. If (independent variables) ==> (Covariance == 0). However, (Covariance == 0) does not necessarily imply those variables are independent.
The Covariance is commutative.
Formula 12. Covariance commutative property.
The Covariance is invariant to the displacement of one or both variables.
Formula 13. The Covariance is invariant to the displacement of the variables.
The Covariance is scaled by each of the scales of X and Y.
Formula 14. The scale of each variable, scales up the Covariance.
Consolidating the two last equations:
Formula 15. Covariance non-linearity property.
The Variance
The Variance is the special case of the Covariance when both variables are the same.
Formula 16. Variance symbols.
The Variance measures how much the values of a random variable are spread out. In other words, how much they are different among them.
Formula 17. Evaluation of Variance from raw data.
We can compute the Variance from the Expected Values of X and its square (X²).
Formula 18. Evaluation of Variance from Expected values.
The Variance of a non-random variable is zero.
Formula 19
The Variance is invariant to the displacement of the variable.
Formula 20.
The displacement of the variable is transparent for the Variance.
If the variable is scaled by a constant (a non-random variable) the Variance gets scaled by the square of that constant.
Formula 21.
The variance is also scaled by the constant but cuadratically.
The Variance of the sum or difference of two correlated random variables is:
Formula 22.
The variance of the sum (and the difference) of two random variables.
If the variables are independent, the Covariance is zero and the Variance of the sum or the difference is the same:
Formula 23.
When the covariance is zero the variance of the sum is equal to the variance of the difference of two random variables.
The Variance of the product of two correlated random variables:
Formula 24. Variance of the product of correlated variables.
Using this relationship between the variance and the expected values we can say "Eva(X²) = Var(X) + Eva²(X)". Using that in the previous formula we get:
Formula 25. Variance of the product of correlated variables.
The Variance of the product of two independent random variables comes from the previous formulas, knowing that in such case $(\sigma_{X,Y} = \sigma_{X^2,Y^2} = 0)$:
Formula 26. Variance of the product of two independent variables.
Another way to get the product of two independent random variables is through this beautiful equation:
Formula 27. The product of two independent variables.
The Standard Deviation
We use the expression StdDev(X) to denote the Standard Deviation of the random variable X.
Formula 28.
Standard Deviation symbols.
The Standard Deviation is the square root of the Variance.
Formula 29. The standard deviation is (by definition) the square root of the Variance.
The Correlation Coefficient
The Correlation Coefficient is a measure of dependence between two —correlated— random variables.
Formula 30. The correlation coefficient.
Analytic Relationship between two Numerically Correlated Functions
Sometimes you can measure two output variables, from an experiment, which are strongly correlated because they come from two functions of a common variable and what you wanna know these two functions. If you build a correlation formula for the relationship between those output variables, with the help of data from many experiments, you can find a good approximation of that correlation formula. However, the question is: How this correlations formula can shed us light about the functions producing those output variables?
Let's suppose, we have $(f(x))$ and $(g(x))$, both evaluated at $(x_i)$ in $({x_1, x_2... x_n})$, which means we have the points $((f(x_i), g(x_i)))$. Now we find a correlation over those points. However, the correlation formula is, of course, between $(f())$ and $(g())$. How can we relate this correlation with $(f(x))$ and $(g(x))$?
To solve this question we will think we are plotting $((z, h(z)))$, then clearly:
\begin{align*} (z, h(z)) &= (f(x_i), g(x_i))\\ \\ z &= f(x) \\ h(z) &= g(x) \\ \\ x &= f^{-1}(z) \\ \therefore h(z) &= g(f^{-1}(z)) \\ \end{align*}
Formula 31. Analytic Correlation between two functions.
Linear case
For example, let's see the case when both, f() and g(), functions are linear:
\begin{align*} ({\bf z}, h({\bf z})) &= (f({\bf x}), g({\bf x})) \\ \\ g({\bf x}) &= g_1 \cdot {\bf x} + g_0 \\ f({\bf x}) &= f_1 \cdot {\bf x} + f_0 \\ \\ {\bf x} &= f^{-1}({\bf z}) \\ {\bf x} &= \frac{{\bf z} - f_0}{f_1} \\ \\ h({\bf z}) &= g(f^{-1}({\bf z})) \\ h({\bf z}) &= g\left(\frac{{\bf z} - f_0}{f_1}\right) \\ h({\bf z}) &= g_1 \cdot \left(\frac{{\bf z} - f_0}{f_1}\right) + g_0 \\ \therefore h({\bf z}) &= \frac{g_1}{f_1} \cdot {\bf z} + \left( g_0 - \frac{g_1}{f_1} \cdot f_0 \right) \tag{32} \end{align*}
Formula 32. Analytic Correlation between two linear functions.
This means that when we correlate two linear functions, the resulting curve is also a line, having as slope the one of $(g(x))$ divided by the one of $(f(x))$. We also know the correlated line crosses the $(h)$ axis (when $(z = 0)$) at $(h = (g_1/f_1) \cdot z + ( g_0 - (g_1/f_1) \cdot f_0 ))$.
We can "validate" this case very easily. Let's suppose our linear functions are:
\begin{align*} f(x) &= 2 \cdot x + 13 \\ g(x) &= 3 \cdot x + 5 \end{align*}
If we plot these functions for $(x)$ in $({1, 2})$ we get $((f, g) = { (15, 8), (17, 11) })$. Knowing those points belong to a line, we can find the slope as $(\Delta y/ \Delta x)$. If our previous deduction is correct, this slope should be equal to $(g_1/f_1 = 3/2)$:
\begin{equation*} slope = \Delta y/\Delta x = (11 - 8) / (17 - 15) = 3/2 \end{equation*}
Which is exactly what we thought!
Also according to our last formula, the interception of the correlated line with $(z = 0)$ should occur when h is:
\begin{align*} h(0) &= (g_1/f_1) \cdot 0 + (g_0 - (g_1/f_1) \cdot f_0) \\ h &= 5 - (3/2) \cdot 13 \\ h &= -14.5 \end{align*}
We can find the interception with $(z = 0)$ from the correlated line data, knowing it contains the point (15, 8):
\begin{align*} (h - 8) &= (3/2) \cdot (z - 15) \\ (h - 8) &= (3/2) \cdot (0 - 15) \\ h &= 8 - (3/2) \cdot 15 \\ h &= -14.5 \end{align*}
Again the result is consistent to our deduction!
Quadratic case
When $(f())$ is linear but $(g())$ is quadratic, we get:
\begin{alignat*}{2} f({\bf x}) &=& &f_1 \cdot {\bf x} + f_0& \cr g({\bf x}) &=&~~g_2 \cdot {\bf x}^2 ~+~ &g_1 \cdot {\bf x} + g_0& \cr \end{alignat*}
\begin{align*} {\bf z} &= f({\bf x}) \cr {\bf x} &= \frac{{\bf z} - f_0}{f_1} \cr \cr h({\bf z}) &= g_2 \cdot \left(\frac{{\bf z} - f_0}{f_1}\right)^2 + g_1 \cdot \left(\frac{{\bf z} - f_0}{f_1}\right) + g_0 \cr \end{align*}
Developing the last equation and summarizing, we finally get:
$$ ({\bf z}, h({\bf z})) = (f({\bf x}), g({\bf x})) $$
\begin{alignat*}{2} f({\bf x}) &=& &f_1 \cdot {\bf x} + f_0& \cr g({\bf x}) &=&~~g_2 \cdot {\bf x}^2 ~+~ &g_1 \cdot {\bf x} + g_0& \cr \end{alignat*}
$$ \begin{align*} \therefore h({\bf z}) &= z_2 \cdot {\bf z}^2 + z_1 \cdot {\bf z} + z_0 \cr \cr z_2 &= \frac{g_2}{f_1^2} \cr z_1 &= \frac{g_1}{f_1} - 2 \cdot \frac{f_0 \cdot g_2}{f_1^2} \cr z_0 &= \frac{g_2}{f_1^2} \cdot f_0^2 - \frac{g_1}{f_1} \cdot f_0 + g_0 \cr \end{align*}\tag{33} $$
Formula 33. Analytic Correlation of a quadratic against a linear function.