Frecuentemente los datos a analizar pueden ser agrupados por uno o más conceptos y es adecuado entender la data desde la perspectiva de dichos grupos. Ejemplos de grupos son el tipo de tratamiento efectuado al paciente, la región donde trabaja el empleado, o el colegio donde estudia un alumno.
Cuando se presenta este caso, una alternativa de análisis es hacer regresiones separadas para cada grupo, pero el problema entonces es que el modelo en cada grupo ignora por completo a las observaciones en los otros. Es decir, se ignora el patrón general de los datos, y hay un sobreajuste (overfitting) cuando hay pocas observaciones en un grupo.
El otro extremo es ignorar los grupos y hacer una sola regresión para todos los datos. Si se incluye el grupo, como un predictor de tipo categórico en la regresión, el resultado es similar al caso mencionado en el párrafo anterior. Si no se incluye el grupo, se ignora la tendencia al interior de cada uno de ellos y entonces hay un sub-ajuste (underfitting), sobre todo cuando hay marcadas diferencias en las observaciones entre grupos.
Las regresiones multinivel incorporan en un mismo modelo tanto la tendencia al interior de cada grupo como el patrón global de los datos.
El resultado de una regresión multinivel incluye la desviación estándar de los coeficientes entre los grupos, permitiendo entender cuando estos grupos son imprescindibles en el modelo. Sin embargo, en el caso en el que las observaciones son homogéneas entre los grupos, y éstos no son imprescindibles, la regresión multinivel revierte automáticamente a una regresión sin grupos.
Deberíamos usar regresiones multinivel como forma de análisis predeterminado.
Algunos estadísticos se refieren a los modelos multinivel con nombres diferentes, algunos refiriéndose a variantes especializadas, y otros usándolos indistintamente. Los sinónimos más comunes de “multinivel” son jerárquicos y de efectos mixtos. Algunos llaman a los coeficientes que varían por grupo "efectos aleatorios" a los globales "efectos fijos" y a la combinación de ellos "efectos mixtos".
- Introducción
- Toy | Variando solo Intercepción en Grupos
- Inferencia Bayesiana Completa
- Toy | Variando solo Intercepción en Grupos (continuación)
- Correlación Intra-Clases
- Regresión Multinivel Requerida
- Toy | Variando Intercepción: Bondad del Ajuste
- Reversión a una Regresión sin Grupos
- Modelo Variando Intercepción y Pendiente
- Modelo "Verdadero" del Conjunto de Datos Toy
- Tipos de Regresiones y de Agrupamiento
- Análisis de Datos de "Junior School Project"
- Corrección de Sesgo
- Influencia de la Escuela en el Progreso Académico del Alumno
- Modelo de Referencia
- Intercepción por Escuela y por Categoría Social
- Hacia el Modelo Final
- Ajuste del Modelo a la Data
- Modelo Final
- Hipótesis= Proposición con Parámetros Estimados
- Efecto de la Escuela en el Alumno
- Clasificación de las Escuelas
- Referencias
- Anexos
Introducción
En una regresión lineal clásica los coeficientes de la regresión son los mismos para todas las observaciones.
\begin{align} y^{(i)} &= \beta_0 + \beta_1 x_1^{(i)} + \beta_2 x_2^{(i)} + \dots + \beta_p x_p^{(i)} +\epsilon^{(i)}, ~para~i=1, ..., N \label{eq:clasLinReg} \\ \epsilon^{(i)} &\sim \mathcal{N}(0, \sigma_{\epsilon}^2) \ \label{eq:linRegEps} \end{align}
En la ecuación \eqref{eq:clasLinReg} $y$ es un vector con los valores de la variable dependiente (llamada también variable de resultado), y la notación para referirse a su valor en la posición indicada por $i$ es $y^{(i)}$. Los vectores tienen forma vertical, son columnas. Las variables ${x_1^{(i)}, x_2^{(i)}, \dots}$ son las predictoras de $y^{(i)}$. En notación más compacta usamos
\begin{aligned} y^{(i)} = {X}^{(i)} {\beta} + \epsilon^{(i)} \label{eq:clasLinRegMat} \end{aligned}
donde ${X}$ es una matriz de dimensiones $N \times p$, es decir con $N$ filas conteniendo cada una los $p$ predictores de cada observación, incluyendo una columna de $1$s para la intercepción, de manera que $X^{(i)}$ son los predictores de la observación en la posición $i$. A su vez $\beta$ es un vector con los coeficientes de la regresión, entonces ${X}^{(i)} {\beta}$ es un vector donde cada fila es el producto interno de predictores por coeficientes. Finalmente, el prerrequisito estándar $\eqref{eq:linRegEps}$ es que los errores $\epsilon^{(i)}$ sean independientes y que estén idénticamente distribuidos con distribución Normal y varianza $\sigma_{\epsilon}^2$.
Las regresiones multinivel (RMN) consideran la posibilidad de que la data puede separarse en grupos donde la regresión entre $y$ y sus predictores varía con el grupo. Por ejemplo, considere el rendimiento de los empleados de una compañía que varía entre oficinas y regiones. Otro ejemplo típico es la nota de alumnos agrupada por salón, curso, o colegio; más adelante estudiaremos un conjunto de datos reales de este tema.
De la misma forma como las regresiones clásicas son extendidas con el modelo linear generalizado (GLM) o aun más con modelo aditivo generalizado (GAM) las regresiones multinivel también son extendidas en esos contextos.
Lo interesante de las RMN es que este agrupamiento no es un prerrequisito. Aunque el diagnóstico de la regresión nos va a decir si el agrupamiento incluido en el modelo es necesario o no, el hecho de que no lo sea, no perjudica a la regresión resultante. Podemos decir que sin agrupamiento significativo la RMN revierte automáticamente a una sin grupos.
Conjunto de Datos "Toy"
Para entender la mecánica de las RMN, practicaremos inicialmente con un conjunto de datos simulados denominado "Toy", posteriormente estudiaremos datos reales. Los datos simulados constan de 504 observaciones de las variables (x, y, g), donde -como ya supondrá- usaremos x como predictora; y como dependiente, y g es una variable categórica con el número del grupo al que pertenece cada observación (puede descargar la data aquí, puede ver el código con el fue generada aquí, y el modelo estadístico detrás aquí). Tenemos 49 grupos, así el valor de g varía entre 1 y 49. El número de observaciones por grupo varía entre 1 y 21 ($n_j$), y el promedio es de 10 observaciones por grupo.
| x | y | g |
|---|---|---|
| 0.273 | 8.9 | 1 |
| 3.308 | 15.6 | 1 |
| 2.720 | 15.2 | 1 |
| 0.617 | 11.6 | 1 |
| 0.252 | 8.0 | 1 |
| 5.337 | 21.3 | 1 |
| 1.735 | 12.4 | 2 |
| 5.413 | 27.1 | 2 |
| 0.147 | 8.8 | 2 |
Toy | Variando solo Intercepción en Grupos
Para introducir la notación de las RMN, digamos que la data puede separarse en $J$ grupos. Inicialmente estudiaremos el caso en el que solo la intercepción de la regresión varía con el grupo:
\begin{align} y^{(i)} = \alpha_0^{(j)} + {X}^{(i)} {\beta} +\epsilon^{(i)} ,~para~i=1, \dots ,N \ \label{eq:rmnInterc} \end{align}
Como en el lado izquierdo de la ecuación \eqref{eq:rmnInterc} tenemos $y^{(i)}$, está implícito que el número de grupo $j$ en $\alpha_0^{(j)}$ se obtiene a partir de $i$, que es el dato de entrada. Es decir, en la matriz de datos hay una columna con el número de grupo de cada observación. En nuestro ejemplo, ésa es la variable g, que contiene número de grupo, por lo que $j=g[i]$. Para denotar esto podríamos usar $\alpha_0^{(g[i])}$ o tal vez $\alpha_0^{(j_i)}$, pero se hace más difícil la lectura de la ecuación y simplemente usamos $\alpha_0^{(j)}$ con la salvedad que acabamos de explicar.
Para ajustar el modelo a los datos podríamos usar el paquete R lme4, que emplea estimaciones puntuales de máxima verosimilitud, y para cálculos con inferencia bayesiana completa podemos usar brms o rstanarm o incluso rstan. La ventaja de lme4 es que es muy rápida y se puede usarse para explorar los datos, pero para el modelo final es recomendable brms o rstanarm, quienes por detrás llaman a stan. En nuestro caso vamos a usar brms. Afortunadamente lme4, brms y rstanarm emplean la misma notación que emplearemos acá.
Para nuestro conjunto de datos, el modelo en la notación de \eqref{eq:rmnInterc} simplemente es
\begin{align} y^{(i)} = \alpha_0^{(j)} + \beta_0 + {\beta_1}{x}^{(i)} +\epsilon^{(i)} ,~para~i=1, \dots ,N \label{eq:rmnIntercEx1} \end{align}
mientras que, el mismo, en la notación de fórmula de brms es
y ~ 1 + x + (1 | g)
donde 1 + x indica que queremos una regresión con intercepción 1 y con x como predictor, comunes a toda la población. Mientras que (1 | g) denota que queremos la intercepción 1 variando por cada grupo en g. El 1 global puede ser omitido, pues por defecto estas fórmulas (en R) asumen que se desea la intercepción, aunque es mejor ser explícito. Mas bien, cuando no se desea intercepción se debe usar -1 o 0 como en y ~ -1 + x + (1 | g) o y ~ 0 + x + (1 | g).
Antes de calcular la regresión de nuestro ejemplo debemos terminar de presentar las ecuaciones que explican cómo es calculado el modelo multinivel. Para ello vamos a darle más generalidad a la ecuación \eqref{eq:rmnInterc}: en vez de $\alpha_0^{(j)}$ vamos a usar $\pmb{\alpha}^{(j)}$ y luego agregar que $\alpha_0^{(j)}$ es su único componente (en este ejemplo):
\begin{align} y^{(i)} &= \pmb{\alpha}^{(j)} + {X}^{(i)} {\beta} +\epsilon^{(i)} ,~para~i=1, \dots ,N \label{eq:rmnIntercF1} \\ \pmb{\alpha}^{(j)} &= \alpha_0^{(j)} + \eta^{(j)}, ~para~j=1, \dots ,J \label{eq:rmnIntercF2} \\ \eta^{(j)} &\sim \mathcal{N}(0, \sigma_\alpha^2) \label{eq:rmnIntercF3} \\ \epsilon^{(i)} &\sim \mathcal{N}(0, \sigma_{\epsilon}^2) \label{eq:rmnIntercF4} \end{align}
El término $\eta^{(j)}$ en las ecuaciones \eqref{eq:rmnIntercF2} y \eqref{eq:rmnIntercF3} nos dice que todas las $J$ intercepciones $\alpha_0^{(j)}$ vienen de una misma distribución (normal) con varianza $\sigma_\alpha^2$. Otra forma de expresar estas dos ecuaciones, condensadas en una sola, es:
\begin{align} \pmb{\alpha}^{(j)} \sim \mathcal{N}(\mu_{\alpha}, \sigma_\alpha^2) \label{eq:muRmnIntc} \end{align}
Note que $\mu_{\alpha}$ y $\sigma_\alpha$ no dependen de $j$, lo cual indica que el origen de todas las intercepciones en los grupos es una misma distribución. Esto traerá beneficios que más adelante comentaremos.
Por otro lado, $\beta$ es el vector con los coeficientes que no varían con los grupos. A menudo se denomina "efectos aleatorios" a la intercepción y coeficientes que varían por grupo. En nuestra notación estos están en $\pmb{\alpha}^{(j)}$, aunque por el momento solo tenemos la intercepción. En esa misma terminología, a la intercepción y variables en ${X}^{(i)}$ se les denomina "efectos fijos", y cuando un modelo tiene ambos efectos dicen que es de "efectos mixtos". Sin embargo, nos referiremos a ellas como a nivel del grupo o de la población (globales), respectivamente.
Con Intercepción a Nivel de Grupo y Población.
Note que el modelo \eqref{eq:rmnIntercEx1} incluye intercepción tanto a nivel población como por grupo ($\beta_0$ y $\alpha_0^{(j)}$). Esto suena a algo redundante, y de hecho lo es. Para resolver esto, el modelo multinivel va a estimar como intercepción a nivel de población a la media de las intercepciones $(\beta_0 = \mu_\alpha)$ y como intercepción a nivel de grupo $\alpha_0^{(j)}$ a la variación por grupo con respecto a esta media. Es decir, en este modelo $\mu_{\alpha}=0$ en la ecuación \eqref{eq:muRmnIntc} .
Ajuste del Modelo a la Data
Ajustaremos el modelo con la función brm() en el paquete brms (del Inglés bayesian regression models using stan). Vamos a usar las distribuciones anteriores (prior distributions) predeterminadas de brms (más adelante hablaremos de estas distribuciones). Luego de ajustar el modelo imprimimos el resumen del ajuste.
brm2_intc <- brm(y ~ 1 + x + (1 | g), data, iter=2500)
summary(brm2_intc)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: y ~ 1 + x + (1 | g)
Data: data (Number of observations: 504)
Samples: 4 chains, each with iter = 2500; warmup = 1250; thin = 1;
total post-warmup samples = 5000
Group-Level Effects:
~g (Number of levels: 49)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 2.96 0.34 2.36 3.69 1.01 535 987
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 9.36 0.47 8.45 10.30 1.03 410 810
x 3.70 0.06 3.58 3.81 1.00 4237 3256
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 2.07 0.07 1.94 2.22 1.00 4317 3699
Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
Note que en el resumen hay tres grandes bloques:
Group-Level Effects: Coeficientes a nivel de grupo, donde nuestro único grupo por la variablegocupa la sección~g.Population-Level Effects: Coeficientes a nivel de población (globales).Family Specific Parameters; Parámetros auxiliares del modelo.
Con los datos en esas secciones podemos ver que la realización de las ecuaciones \eqref{eq:rmnIntercF1}-\eqref{eq:rmnIntercF4}, para nuestro modelo es:
\begin{align*} y^{(i)} &= \pmb{\alpha}^{(j)} + 9.36 + 3.70 x +\epsilon^{(i)} ,~para~i=1, \dots ,504 \\ \pmb{\alpha}^{(j)} &= \alpha_0^{(j)} + \eta^{(j)}, ~para~j=1, \dots ,49 \\ \eta^{(j)} &\sim \mathcal{N}(0, 2.96^2) \\ \epsilon^{(i)} &\sim \mathcal{N}(0, 2.07^2) \end{align*}
Antes de ver más detalles de qué hemos obtenido al ajustar el modelo con inferencia Bayesiana completa, necesitamos entender mejor en qué consiste ésta y cómo se analizan sus resultados.
Inferencia Bayesiana Completa
Como brms ajusta modelos usando inferencia Bayesiana completa, varios de los pasos siguientes en este artículo refieren a términos y análisis propios de ese enfoque. Vamos a hacer un alto al modelado y en esta sección vamos a revisar este tema, que puede saltar si ya está familiarizado con esto. ¡Si no es así, bienvenido! Está en un buen lugar para aprender esto desde cero. Al principio el tema es un poco denso. Por favor tenga paciencia y en breve verá como todas las piezas encajan.
Modelo de Datos eCompo
En esta sección usaremos un conjunto de datos denominado "eCompo". Se trata de una serie de lecturas "$x$" de un componente electrónico, que en una prueba ha sido sometido a diferentes valores de un estímulo "$y$". Queremos conocer los dos parámetros $\beta$ y $\sigma_\epsilon$ en el modelo que se muestra a continuación:
\begin{align} y &= \beta \cdot x + \epsilon \\ \epsilon &\sim \mathcal{N}(0, \sigma_{\epsilon}^2) \label{eq:demoPostLik} \\ \implies y - (\beta \cdot x) &\sim \mathcal{N}(0, \sigma_{\epsilon}^2) \label{eq:demoPostEps} \end{align}
La distribución esperada de los residuos \eqref{eq:demoPostLik} tiene la varianza de éstos, pero está centrada en cero. Es decir, se espera que el centro de los residuos sea cero. Vamos a estimar la varianza $\sigma_{\epsilon}^2$ con la de los residuos en la data.
Ejercicio para la Intuir la Probabilidad Conjunta
En el gráfico "Beta vs Residuos" (abajo), se muestra con color verde la distribución esperada de los residuos, y con morado su distribución real $\epsilon = y - (\beta \cdot x)$ según la data. Con $\beta=9.3$ en (1) los residuos se aproximan a la distribución esperada. Conforme $\beta$ se incrementa, como hasta $\beta=15.3$ en (2), los residuos se esparcen y su centro se mueve hacia la izquierda, alejándose de lo esperado. Como su varianza aumenta, su distribución esperada se aplana tratando de seguirlos, pero el calce es cada vez peor: la distribución real es cada vez más diferente a la esperada. En este último caso decimos que $\beta=15$ "hace poco probable observar los datos que tenemos".
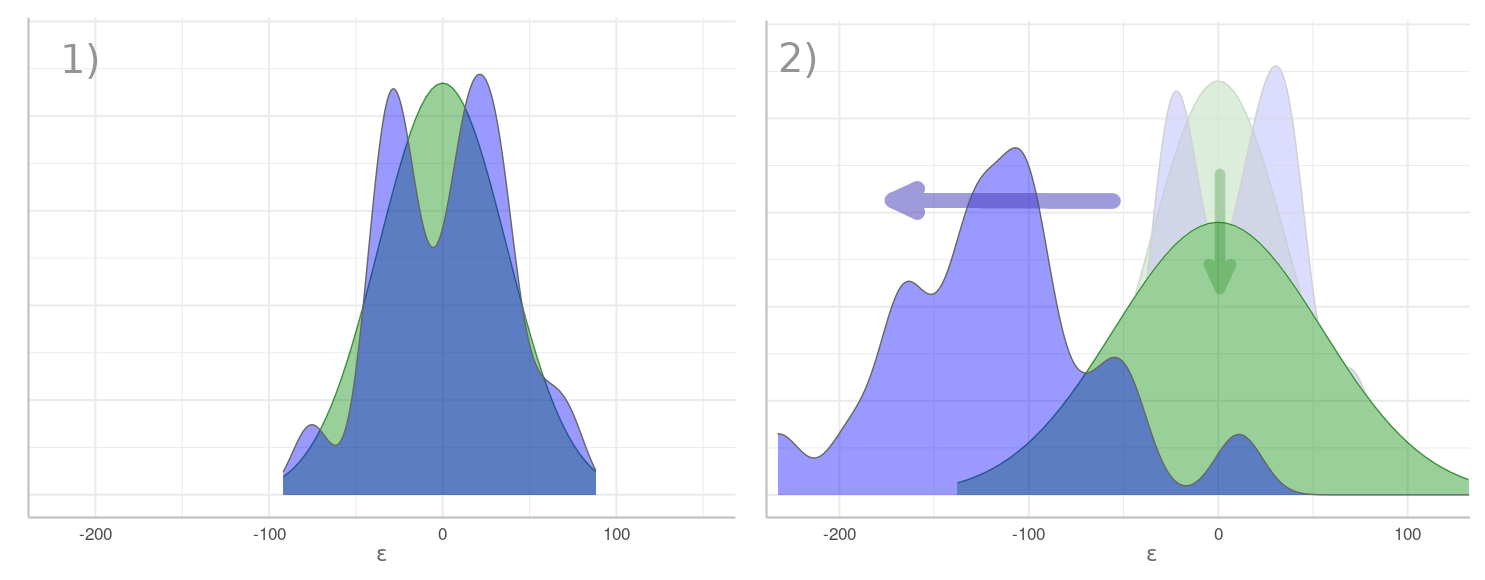
Beta vs Residuos. En verde se muestra la distribución esperada de los residuos según \eqref{eq:demoPostLik}: con centro en cero y la varianza de éstos. En morado su distribución real. En el momento (1) el valor de $\beta$ produce residuos cuya distribución es relativamente acorde a la esperada. En (2) valores crecientes de $\beta$ causan residuos cada vez más negativos con una varianza creciente. Su distribución esperada se aplana tratando de seguir a los residuos, pero el calce es cada vez menor.
La idea de este ejercicio es motivar la intuición de que los parámetros de un modelo tienen la distribución conjunta de la probabilidad de observar la data según el modelo. Cuando movemos uno o más parámetros, usamos la data que tenemos para ver como varía "la probabilidad de verla" según el modelo. Esto es, analizamos la probabilidad conjunta de los parámetros "condicionados a la data".
Aun cuando en el sumario de brm() hemos visto estimaciones puntuales de los parámetros de nuestro modelo eCompo, en realidad los ha calculado a partir de muestras de la distribución conjunta de esos parámetros condicionados a la data. Veamos a continuación como obtener esa distribución.
La expresión formal de la probabilidad conjunta de los parámetros de nuestro modelo multinivel ( $\alpha_0^{(j)}, \beta, \sigma_\alpha, \sigma_{\epsilon}$) condicionada a la data ($y, X$) es:
$$\begin{aligned} \pi(\alpha_0^{(j)}, \beta, \sigma_\alpha, \sigma_{\epsilon} \mid y, X) \end{aligned}$$
Notación Simplificada
Por simplicidad, llamaremos $\theta$ al vector con todos los parámetros del modelo. A su vez, con $y$ representaremos a toda la data, así que $X$ estará también implícita. Finalmente, en estas expresiones, $\pi(\cdot)$ es la función de densidad de $(\cdot)$, es decir es una función diferente para cada $(\cdot)$ diferente, que corresponde a una función de masa en el caso discreto. Usaremos el término distribución con el mismo sentido que función de densidad.
Con esta notación simplificada, lo que buscamos es:
$$\begin{aligned} \pi(\theta \mid y) \end{aligned}$$
Por la regla de Bayes sabemos que:
\begin{align} \pi(\theta \mid y) &= \frac{\pi(y, \theta)}{\pi(y)} = \frac{\pi(y \mid \theta) \cdot \pi(\theta)}{\pi(y)} \label{eq:posterior} \\ \pi(\theta \mid y) &\propto \pi(y \mid \theta) \cdot \pi(\theta) \label{eq:propPost} \end{align}
En \eqref{eq:posterior}, el numerador es la probabilidad conjunta de los parámetros y la data, a la cual nos hemos referido en el ejercicio anterior. El denominador $\pi(y)$ es una constante que no depende de $\theta$ sino solo de la data, por lo que $\pi(\theta \mid y)$ en \eqref{eq:propPost} es proporcional al numerador de \eqref{eq:posterior}. Podemos considerar el lado derecho \eqref{eq:propPost} como la distribución no normalizada de $\pi(\theta \mid y)$, es decir cuya integral no es igual a $1$.
La ecuación \eqref{eq:propPost} es clave en la inferencia Bayesiana, y cada término tiene un nombre al que nos referiremos frecuentemente.
- $\pi(\theta)$ es la distribución "anterior" (prior distribution): la que asumimos tienen los parámetros antes de ver la data. Nos referiremos a esta distribución como anterior o prior.
- $\pi(y \mid \theta)$ es la distribución de muestreo de la data (sampling distribution). Aquí miramos este término como función de $\theta$, pues la data $y$ se mantiene constante, y en ese sentido este término es llamado la "verosimilitud" (likelihood) de nuestro modelo.
- $\pi(\theta \mid y)$ es la distribución "posterior": Es la distribución de los parámetros condicionados a la data. A la que nos referimos como la probabilidad de ver la data que tenemos, con el modelo y parámetros que tenemos.
Como $\theta$ es un vector, estos términos corresponden a distribuciones conjuntas de probabilidad de todos ellos. Por no haber aun introducido la distribución "anterior", implícitamente nos hemos referido a la verosimilitud cuando hemos hablado de la "posibilidad de observar la data" en el ejercicio anterior, que corresponde al caso cuando la distribución anterior es uniforme.
Ejemplo de Inferencia Bayesiana sin Stan
En esta sección veremos un ejemplo práctico de los conceptos introducidos en la sección anterior, analizando numéricamente (sin usar directa ni indirectamente stan) el modelo eCompo.
Distribución Anterior
Los expertos que hemos consultado nos dicen que $\beta$ debe de estar —a lo mucho— entre $1$ y $25$, con una distribución aproximadamente Normal, lo cual implica su centro en $(25+1)/2=13$, con una desviación estándar (al 95%) de $(25-1)/4=6$, por lo que asumimos como anterior de $\beta$ una distribución Normal con esos parámetros. Los expertos también nos dicen, que la distribución Exponencial es adecuada como prior de una desviación estándar usando como parámetro $\lambda$ de la misma al recíproco de la desviación estándar de $y$, por lo que adoptamos como anterior de $\sigma_\epsilon$ a tal distribución con $\lambda=1/sd(y)$.
El prior $\pi(\theta)$ de este modelo es:
prior_beta_mean <- 13
prior_beta_sd <- 6
prior_sigma_lambda <- 1 / sd(y)
prior_density <- function(beta, sigma, log = TRUE) {
log_prior_beta <- dnorm(beta, mean = prior_beta_mean, sd = prior_beta_sd, log = TRUE)
log_prior_sigma <- dexp(sigma, rate = prior_sigma_lambda, log = TRUE)
result <- log_prior_beta + log_prior_sigma
if (log != TRUE) result <- exp(result)
return(result)
}
Donde beta y sigma en el código corresponden a $\beta$ y $\sigma_\epsilon$ en nuestro modelo. Como estos parámetros son independientes, su prior conjunto es el producto de los priors de cada parámetro. Tal como vimos, esta distribución no depende de los datos, sino solo de $\theta$, y de los hiper-parametros con los que modelamos los priors individuales (como prior_beta_sd o prior_sigma_lambda), que forman parte de nuestro modelo. Como un tema meramente técnico (estabilidad y precisión numérica), los cálculos son hechos en el espacio logarítmico.
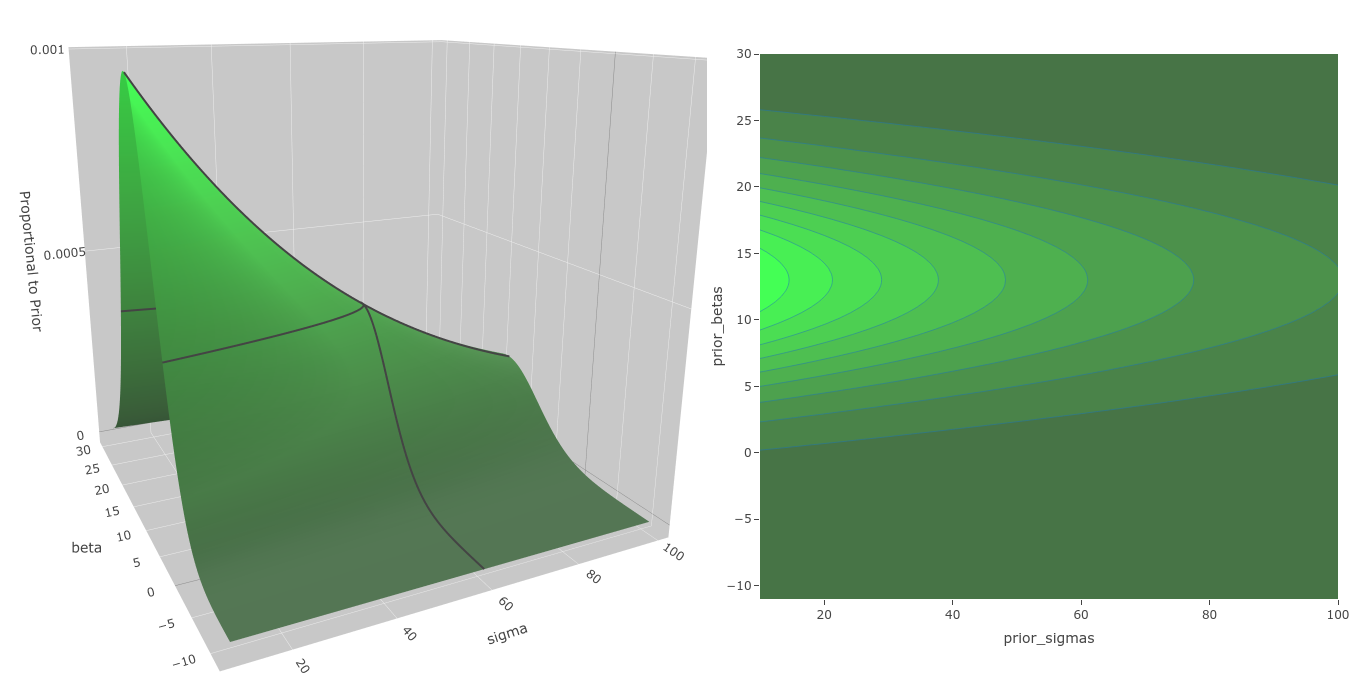
Distribución Anterior. La distribución anterior cubre el área de valores plausibles de los parámetros del modelo.
Una distribución anterior debe cubrir con holgura el dominio de los posibles valores de los parámetros, que en el el gráfico "Distribución Anterior" (arriba) vemos como ocurre en nuestro ejemplo.
Distribución de Verosimilitud
La distribución de la verosimilitud $\pi(y \mid \theta)$ es:
likelihood_density <- function(beta, sigma, y, x, log = TRUE) {
result <- 0
for (i in seq_along(y)) {
mean <- beta * x[i]
result <- result + dnorm(y[i], mean = mean, sd = sigma, log = TRUE)
}
if (log != TRUE) result <- exp(result)
return(result)
}
Como esperábamos, la verosimilitud es función tanto de la data como de $\theta$. En nuestro modelo, la ecuación \eqref{eq:demoPostLik} define la probabilidad de ver cada observación en la data. Como éstas son independientes su probabilidad conjunta es el producto de la verosimilitud de todas las observaciones.
Note que, estrictamente hablando, likelihood_density() y prior_density() son funciones de densidad no normalizadas. Para que sean normalizadas se requiere que la integral, con respecto $\theta$, de los valores que produce cada una de ellas sea $1$. Por ejemplo, en el caso de la distribución anterior, esto es $\int_{-\infty}^{+\infty} \pi(\theta)~\textrm{d}\theta = 1$, lo cual no es cierto. Solo falta dividir el resultado de cada función por el valor de su integral. Más adelante nos ocuparemos de esto.
Distribución Conjunta
Con lo calculado anteriormente, la distribución conjunta $\pi(y \mid \theta) \cdot \pi(\theta)$ es trivial:
joint_density <- function(beta, sigma, data, log = TRUE) {
result <-
prior_density(beta, sigma, log = TRUE) +
likelihood_density(beta, sigma, data$y, data$x, log = TRUE)
if (log != TRUE) result <- exp(result)
return(result)
}
Distribución Posterior
La distribución conjunta $\pi(y \mid \theta) \cdot \pi(\theta)$ calculada por la función joint_density() es todo lo que necesitamos en \eqref{eq:propPost}. Aun así vamos a calcular $\pi(y)$, mostrando que no es más que la integral de joint_density() sobre $\theta$, una constante con la que la dividiremos para normalizarla y obtener así la distribución de densidad posterior $\pi(\theta \mid y)$ según \eqref{eq:posterior}.
$$\begin{aligned} \pi(y) &= \int_{-\infty}^{+\infty} \pi(y \mid \theta) \cdot \pi(\theta)~\textrm{d}\theta \\ \pi(y) &= \int_0^{+\infty} \int_{-\infty}^{+\infty} \textrm{joint_density}(\beta, \sigma_\epsilon \mid data)~\textrm{d}\beta~\textrm{d}\sigma_\epsilon \end{aligned}$$
La distribución posterior $\pi(\theta \mid y)$ tiene la forma:
posterior_density <- function(beta, sigma, data, log = TRUE) {
result <- joint_density(beta, sigma, data, log = TRUE) - log(pi_y)
if (log != TRUE) result <- exp(result)
return(result)
}
Donde pi_y es el valor de la integral que debemos calcular, es decir corresponde a $\pi(y)$. Tenemos la dificultad de que cuando integramos pi_y = 1 la función posterior_density() retorna valores menores que $3.4 \times 10^{-47}$ y la integración es numéricamente inestable, por lo que vamos a asignarle a pi_y un valor temporal mientras integramos y luego ajustaremos su valor con el resultado de la integral.
pi_y <- 3.4e-47
int_pi_y <- integrate(function(sigmas) {
sapply(sigmas, function(sigma) {
integrate(
function(beta) posterior_density(beta, sigma, data, log = F),
-Inf, +Inf
)$value
})
}, 0, +Inf)$value
pi_y <- pi_y * int_pi_y
El valor final es $\pi(y)=2.798 \times 10^{-46}$, con lo que posterior_density() es ahora una función de densidad normalizada. Ahora podemos regresar al ejercicio inicial y calcular la probabilidad de (1) $\pi(\beta=9.3, \sigma_\epsilon=36.6 \mid y)=0.071$ y de (2) $\pi(\beta=15, \sigma_\epsilon=55.1 \mid y)=1.6 \times 10^{-25}$. Donde vemos que es practicamente imposible observar la data que tenemos con $\beta=15$.
Gráfico de la distribución Posterior
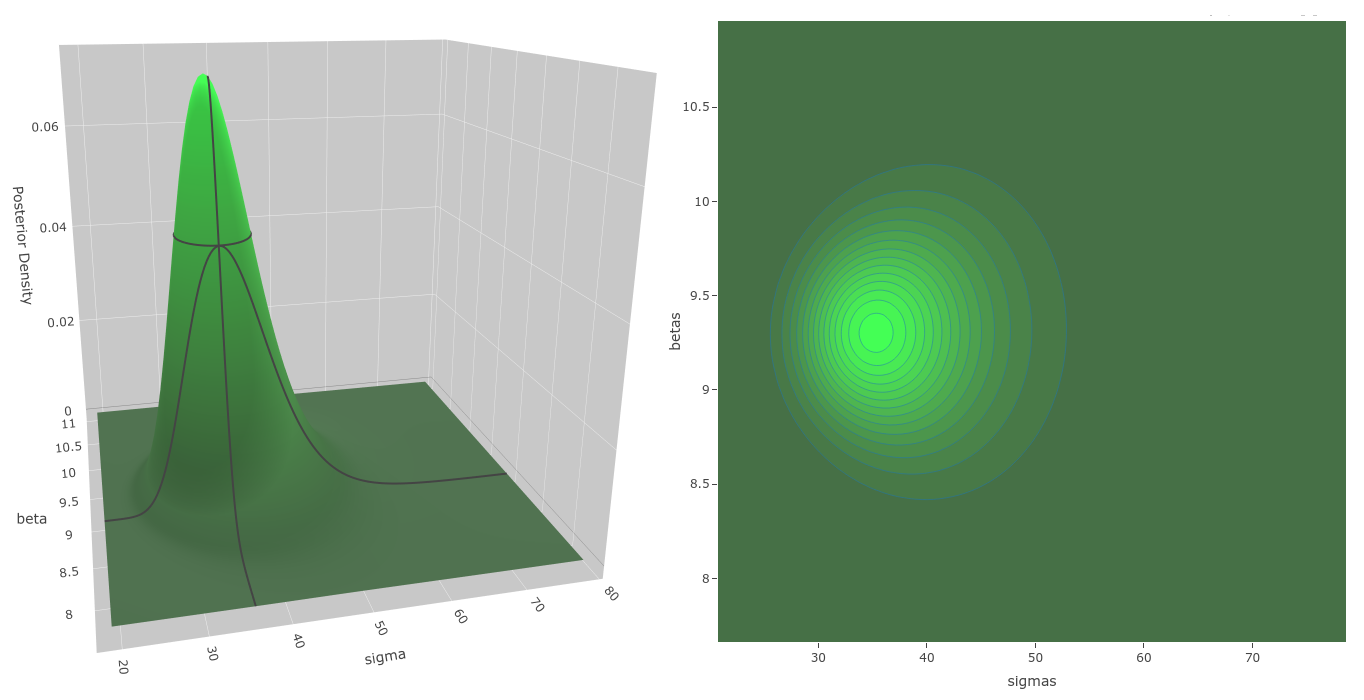
Distribución Posterior. Distribución posterior calculada numéricamente, con algunas líneas de contorno para notar mejor su forma. Puede verse que $\sigma_\epsilon$ tiene una cola más larga a la derecha.
En el gráfico "Proporcional al Posterior" (arriba), vemos que en nuestro caso $\pi(\theta)$ tiene un punto modal prominente. Algunos algoritmos de estimación puntual de tipo máxima verosimilitud estiman la posición de esta moda como solución a los parámetros del modelo. En una estimación Bayesiana eso corresponde a la moda de la posterior cuando los priors son uniformes, pero nosotros no usamos solo las estimaciones puntuales de $\theta$, sino toda su distribución, incorporando en nuestros cálculos la incertidumbre que el modelo tiene acerca de su valor.
Es posible obtener la posición de la moda de la posterior usando la función optimizing() de rstan. En nuestro caso podemos hallarla con un optimizador numérico en R.
res <- nlm(function(theta) -posterior_density(theta[1], theta[2], data), c(7, 11))
res
$minimum
[1] 2.61698
$estimate
[1] 9.303106 35.262023
$gradient
[1] -1.038726e-07 -6.448118e-09
Como nlm (Non-Linear Minimization) calcula mínimos, invertimos el signo de posterior_density. Asimismo, como log es una función monotónica optimizamos en el espacio logarítmico por conveniencia numérica. Obtenemos $\beta=9.3031$ y $\sigma_\epsilon=35.2620$.
Comparación con Ajuste Obtenido con Stan
En este artículo, obtendremos muestras de la posterior con el apoyo de stan, mediante brms. A continuación, vamos a ajustar el modelo eComp directamente con stan (y no vía brms) para mejor control de todos los detalles.
library(rstan)
options(mc.cores = parallel::detectCores())
rstan::rstan_options(auto_write = TRUE)
model.stan <- "
data {
int<lower=2> N;
vector[N] x;
vector[N] y;
real prior_beta_sd;
real prior_beta_mean;
real<lower=0> prior_sigma_lambda;
}
parameters {
real beta;
real<lower=0> sigma;
}
model {
vector[N] mu;
beta ~ normal(prior_beta_mean, prior_beta_sd);
sigma ~ exponential(prior_sigma_lambda);
mu = beta * x;
y ~ normal(mu, sigma);
}
"
data.stan <- list(
N = length(y),
x = x,
y = y,
prior_beta_sd = prior_beta_sd,
prior_beta_mean = prior_beta_mean,
prior_sigma_lambda = prior_sigma_lambda
)
fit.stan <- stan(model_code = model.stan, data = data.stan, chains=4, iter=2250, warmup=1000 ,refresh = 0)
stan_samples <- as.data.frame(fit.stan)
summary(fit.stan, probs=c(.25,.50,.75))$summary %>% print(digits=4)
mean se_mean sd 25% 50% 75% n_eff Rhat
beta 9.305 0.006899 0.3983 9.035 9.312 9.568 3332 1
sigma 38.647 0.121053 6.7265 33.899 37.826 42.289 3088 1
lp__ -104.999 0.025306 1.0639 -105.401 -104.684 -104.250 1768 1
En nuestro código arriba, la variable stan_samples contiene las $5000$ muestras recibidas de stan, que está compuesta de los valores de las variables beta, sigma y lp__, tal como puede verse en el listado de salida. En stan_samples, la variable lp__ contiene el logaritmo de la posterior de nuestro modelo más los ajuste por los Jacobianos requeridos para pasar parámetros de una escala restringida a una no restringida. En nuestro caso $\sigma_\epsilon$ es la única variable restringida (a ser positiva), lo cual compensamos restando su logaritmo.
Si lo anterior no quedó muy claro, digamos que lp__ no es exactamente el logaritmo de la posterior como la calculamos nosotros, sino que contiene además ciertas adiciones de stan que debemos deshacer antes de poder compararla con la que calculamos nosotros.
lpd_num <- purrr::map2_dbl(
stan_samples$beta, stan_samples$sigma,
function(beta, sigma) posterior_density(beta, sigma, data)
)
plot_data <- data.frame(
lpd_num = lpd_num,
lpd_stan = stan_samples$lp__,
beta = stan_samples$beta,
sigma = stan_samples$sigma
) %>%
mutate(
diff = lpd_num - (lpd_stan - log(sigma))
)
sd(plot_data$diff)
[1] 3.235096e-14
En el código arriba, en lpd_num calculamos el logaritmo de la posterior para los pares de $\beta$ y $\sigma_\epsilon$ en las muestras devueltas por stan, a fin de comparar el resultado de nuestros cálculos con los de stan en lp__. Al calcular en diff la diferencia entre los logaritmos de las posteriores, a la de stan le restamos el logaritmo de sigma por la razón comentada antes. Luego de eso, ambos logaritmos deberían diferir solo por una constate, lo cual verificamos es lo que ocurre, pues la desviación estándar de tal diferencia es prácticamente cero.
En otras palabras, nuestros cálculos de la posterior, verosimilitud y posterior coinciden perfectamente con los que hace stan ✅.
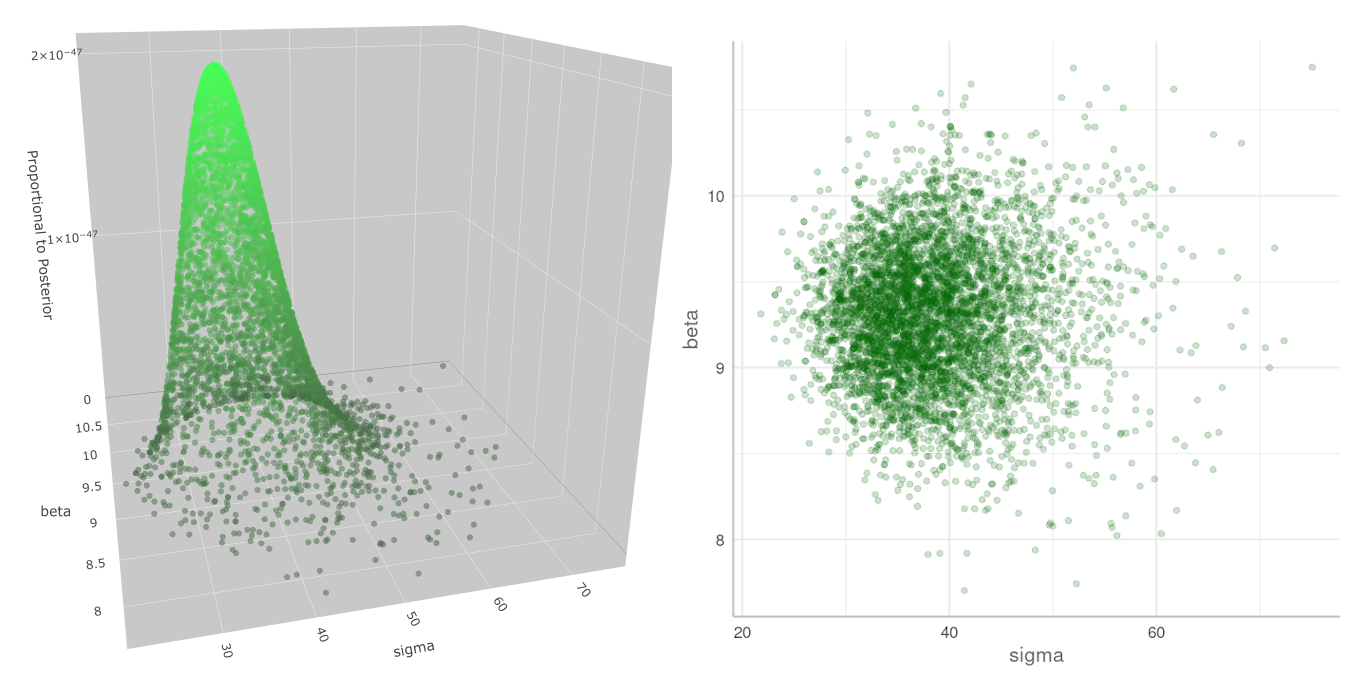
Proporcional al Posterior. Muestras recibidas de stan. La distribución calculada por stan es igual a la que calculamos nosotros y mostramos en el gráfico anterior. La escala vertical aquí es diferente a la nuestra debido a que ésta es calculada con \eqref{eq:propPost} y la nuestra con \eqref{eq:posterior}.
La distribución hallada por stan es igual a la que calculamos nosotros y mostramos en el gráfico "Distribución Posterior" (más arriba). La escala vertical aquí es diferente a la nuestra, pues aquí corresponde a \eqref{eq:propPost} y la nuestra a \eqref{eq:posterior}. Aunque eso es irrelevante, pues lo que importa es la posición de las muestras en el espacio de $\theta$.
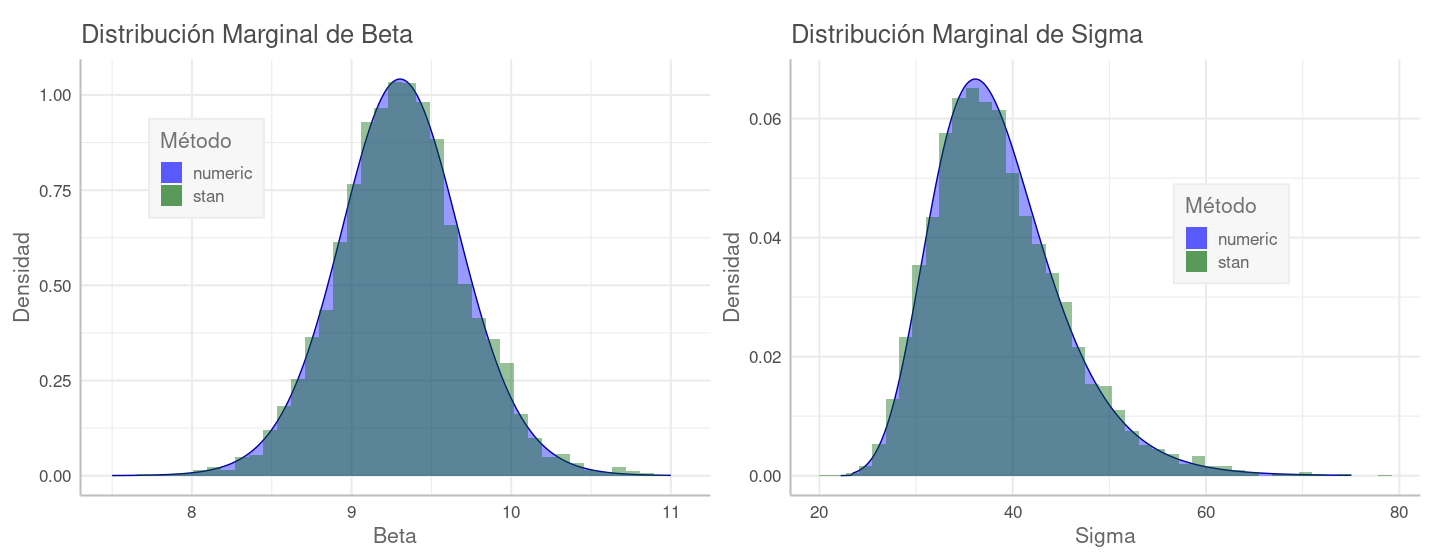
Distribución Marginal
Si bien los parámetros tienen una distribución conjunta, es decir el valor de cada uno condiciona el de los demás, podemos obtener su distribución marginal integrando la distribución conjunta posterior sobre los demás parámetros.
\begin{align*} \pi(\beta) &= \int_0^{+\infty} \textrm{posterior_density}(\beta, \sigma_\epsilon \mid data) ~\textrm{d}\sigma_\epsilon \\ \pi(\sigma_\epsilon) &= \int_{-\infty}^{+\infty} \textrm{posterior_density}(\beta, \sigma_\epsilon \mid data)~\textrm{d}\beta \end{align*}
Integramos numéricamente la distribución posterior para obtener las marginales, luego las graficamos, comparándolas con los valores obtenidos con stan:
sigma_density <- function(sigmas) {
sapply(sigmas, function(sigma) {
integrate(function(beta) posterior_density(beta, sigma, data, log = F), -Inf, +Inf)$value
})
}
# Asegurar el area bajo la curva integrada sea igual a 1
sigmas <- seq(22.2, 75, length.out = 200)
plot_sigma <- data.frame(sigma=sigmas, dens=sigma_density(sigmas))
diffs <- diff(sigmas)
diffs <- c(diffs[1], diffs)
area <- sum(diffs * plot_sigma$dens)
plot_sigma$dens <- plot_sigma$dens/ area
plot_sigma %>%
ggplot() +
geom_line(aes(sigma, dens), color = "darkblue") +
geom_ribbon(
aes(sigma, ymax = dens, fill = "numeric"),
ymin = 0, alpha = 0.4
) +
geom_histogram(
data = stan_samples,
aes(x= sigma, y = ..density.., fill = "stan"), alpha = 0.4, bins=45
) +
scale_fill_manual(values = c("numeric" = "blue", "stan" = "darkgreen")) +
labs(
title = "Distribución Marginal de Sigma",
x = "Sigma",
y = "Densidad"
) +
labs(fill="Método") +
theme(legend.position = c(0.7, 0.6))
Estas curvas muestran que la densidad de las muestras que devuelve stan es proporcional a la de la distribución de la posterior. Esta es una propiedad importante que aprovecharemos en la siguiente sección.
Estimación del Valor Esperado de los Parámetros
Calcularemos numéricamente los valores esperados de $\beta$ y $\sigma_\epsilon$ ($\mu_\beta$ y $\mu_{\sigma_\epsilon}$ respectivamente) para compararlos con los valores estimados con las muestras de stan.
$$ \mu_\beta = \int_0^{+\infty} \int_{-\infty}^{+\infty} \beta \cdot \pi(\beta, \sigma_\epsilon \mid y) ~\textrm{d}\beta~\textrm{d}\sigma_\epsilon $$
stan_beta_mu <- stan_summary["beta", "mean"]
stan_sigma_mu <- stan_summary["sigma", "mean"]
stan_beta_mu_se <- stan_summary["beta", "se_mean"]
stan_sigma_mu_se <- stan_summary["sigma", "se_mean"]
beta_mu <- integrate(function(sigmas) {
sapply(sigmas, function(sigma) {
integrate(
function(beta) beta * posterior_density(beta, sigma, data, log = F),
-Inf, +Inf
)$value
})
}, 0, +Inf)$value
sigma_mu <- integrate(function(sigmas) {
sapply(sigmas, function(sigma) {
integrate(
function(beta) sigma * posterior_density(beta, sigma, data, log = F),
-Inf, +Inf
)$value
})
}, 0, +Inf)$value
(stan_beta_mu - beta_mu) / stan_beta_mu_se
(stan_sigma_mu - sigma_mu) / stan_sigma_mu_se
[1] -0.1928841
[1] 0.4831648
La herramienta de integración numérica que usamos nos dice que esos estimados tienen al menos 4 dígitos decimales de precisión. Asimismo, como referencia, hemos ajustado el modelo con una regresión lineal clásica (columna lm). Los parámetros del modelo que usamos para simular esta data se muestran en la columna source_value y la posición de la moda está en post_mode.
parameter stan_mean stan_se numeric_mean lm source_value post_mode
beta 9.3048 0.0069 9.3062 9.2898 8.9 9.3031
sigma 38.6470 0.1211 38.5885 36.6511 30.4 35.2620
Si no tuviéramos un estimado más preciso del valor de los parámetros, asumiríamos que el error absoluto debe de ser menor que dos errores estándar stan_se (al $97.7\%$), siguiendo una distribución normal. Comparados con nuestros estimados, los errores en los de stan son apenas $-0.19$ y $0.48$ errores estándar. Es decir, los errores stan_se son estimados conservadores, tal como lo afirma su documentación.
La media de empírica de nuestros parámetros, calculada con los valores de las muestras de stan, se aproxima a la esperanza de sus valores a medida que las muestras tienen una densidad proporcional a la de la posterior y corresponden a muestras independientes tomadas de la misma. El número efectivo de muestras independientes que hemos obtenido de stan está representado por la variable n_eff que aparece en sus estimados.
Aplicación de la Distribución Posterior
La gran ventaja de tener la distribución posterior de los parámetros es que podemos derivar cualquier expresión que dependa de ellos. Por ejemplo, supongamos que queremos saber en nuestro modelo si es posible que $y$ para $x=24$ puede llegar a ser mayor que su valor para $x=28$ considerando tanto la distribución de muestreo de $y$ como la incertidumbre que tenemos de los parámetros.
y_density <- function(x) {
map2_dbl(
stan_samples$beta * x, stan_samples$sigma,
function(mu, sd) rnorm(1, mu, sd)
)
}
y_22 <- y_density(x=22)
y_28 <- y_density(x=28)
mean(y_22 > y_28)
[1] 0.1532
La respuesta es, sí es posible, y puede ocurrir en el $15\%$ de los casos. ¿Cómo calcularía algo así con una estimación puntual clásica?
Conclusión
Hemos necesitado usar un ejemplo trivial, solo para que nos permita mostrar en un solo gráfico la distribución posterior y podamos tener la noción de que lo que hace stan es exactamente lo que hemos descrito aquí. Sin embargo, nosotros hemos "hallado" la distribución con una cuadrícula de $100 \times 100$ puntos, pero no hemos muestreado los parámetros de allí, los hemos calculado mediante integrales evaluadas numéricamente. Más adelante resolveremos un modelo con $227$ parámetros, y un análisis con cuadrícula sería imposible, requería $100^{227}=10^{454}$ puntos y tendríamos que calcular integrales múltiples con $227$ niveles (orden) y aun si llegáramos a poder plantear algo así ¿cuánto tiempo de ejecución se requería?.
Stan es una plataforma de alto rendimiento para el modelado estadístico, que obtiene muestras de los valores de los parámetros, tomadas de la distribución posterior del modelo.
Toy | Variando solo Intercepción en Grupos (continuación)
En las primeras secciones ajustamos el modelo "variando solo intercepción por grupo" a la data del conjunto de datos Toy. Aquí revisamos lo que hicimos y continuamos el análisis.
Distribución Posterior obtenida con Stan
En esta sección anterior ajustamos el modelo a la data usando la función brm() y obtuvimos este listado. La función brm() transformó nuestra formula y ~ 1 + x + (1 | g) en un modelo en código stan, incluyendo en él las distribuciones anteriores por defecto de brms. Con ése código y nuestra data, brm() llamó a stan para que "ajuste" el modelo a la data. La función brm() recibió de stan $5000$ muestras de la distribución posterior de los parámetros de nuestro modelo \eqref{eq:rmnIntercEx1} y en base a estas calculó los parámetros reportados en el listado mencionado.
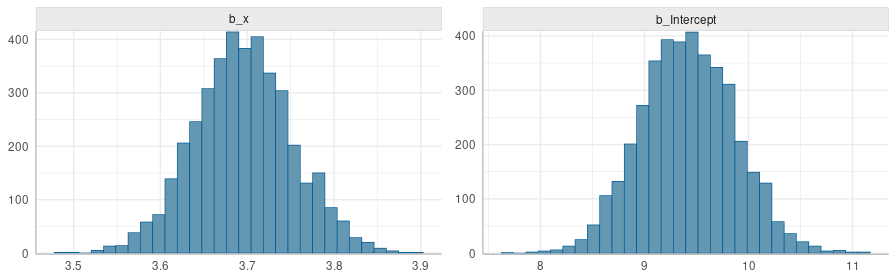
Distribución posterior de los coeficientes $\beta_0$ y $\beta_1$ del modelo en \eqref{eq:rmnIntercEx1}.
La cantidad de muestras que se obtienen depende de los parámetros chains, iter y warmup en el llamado a brm(): $nsamples=chains \times (iter-warmup)$, en nuestro caso =4*(2500-1250)=5000.
Siempre existe la posibilidad de que stan no pueda recorrer satisfactoriamente todo el espacio muestral de los parámetros, y que por ello las muestras que retorne no sean representativas de la verdadera distribución posterior. Para mantenernos al tanto de eso stan emite estadísticas como Rhat y Bulk_ESS que aparecen en el sumario (para más detalles vea Brief Guide to Stan’s Warnings). Lo deseable es que Rhat sea menor que 1.1, siendo 1 su mejor valor posible. Tail_ESS y Tail_ESS deben ser mayor que $100 \times chains$; en nuestro ajuste usamos iter = 2500 pues con su valor por defecto 2000 no pasábamos estos chequeos, ahora todo está bien ✅.
Estimaciones de los Parámetros
El paquete R brms nos permite obtener la distribución de cada parámetro, pero también permite obtener directamente una estimación puntual de cada parámetro del modelo, que por simplicidad es lo que vamos a usar en este ejemplo.
Los coeficientes a nivel de población están en el sumario, pero no aquellos a nivel de grupo, como $\alpha_0^{(j)}$ en nuestro modelo. Con la función ranef() (random effects: efectos aleatorios) se puede obtener el coeficiente para cada grupo, y con fixef() (fixed effects: efectos fijos ) los coeficientes a nivel población, mientras que los estimados consolidando ambos orígenes se obtienen con coef().
Por ejemplo, en nuestro ajuste la intercepción a nivel población es $9.36$ (fixef(): $\beta_0$) y la intercepción de los grupos 1 y 2 es $-3.34$ y $-2.31$ (ranef(): $\alpha_0^{(1)}$ y $\alpha_0^{(2)}$), entonces la intercepción consolidada de estos dos grupos es $6.01$ y $7.04$ (coef(): $\alpha_0^{(j)} + \beta_0$), pues $6.01= 9.36-3.34$ y $7.04= 9.36-2.31$.
coef(brm2_intc)
$g
, , Intercept
Estimate Est.Error Q2.5 Q97.5
1 6.009167 0.8352279 4.409063 7.671721
2 7.046681 0.4624261 6.146496 7.931515
3 10.660634 0.5802230 9.518355 11.818091
:
, , x
Estimate Est.Error Q2.5 Q97.5
1 3.696783 0.0568952 3.585757 3.807682
2 3.696783 0.0568952 3.585757 3.807682
3 3.696783 0.0568952 3.585757 3.8076
:
[truncado por razones de espacio]
Correlación Intra-Clases
Una pregunta relevante en RMN es ¿cuanta variación hay entre los grupos comparada con la variación entre individuos de la población? Esta proporción es medida por la correlación intraclases (ICC: intraclass correlation):
\begin{equation} ICC = \frac{\sigma_\alpha^2}{\sigma_\alpha^2 + \sigma_{\epsilon}^2} \label{eq:icc} \end{equation}
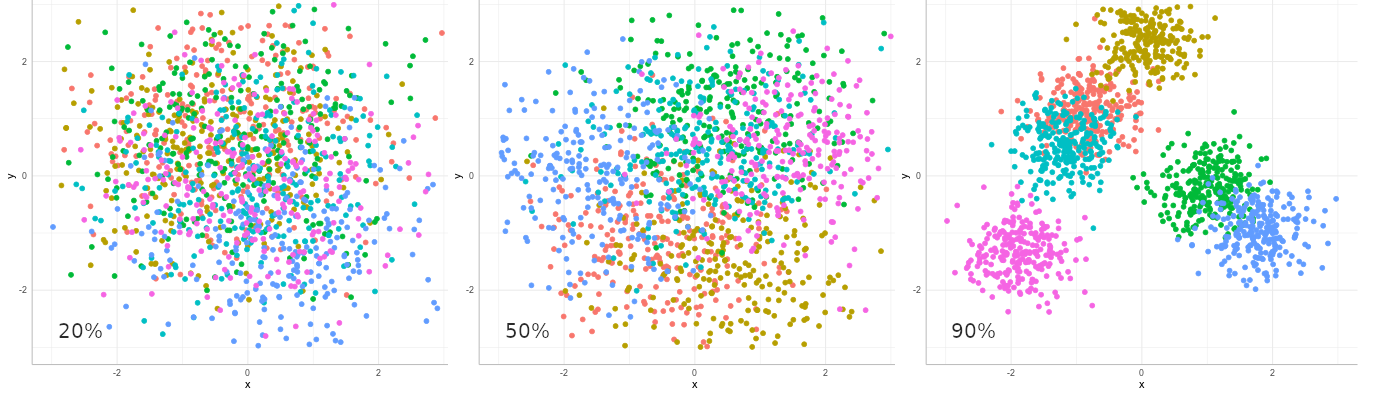
ICC es la proporción de la varianza en la variable de resultado $y$ que puede ser explicada por la varianza entre grupos. En nuestro modelo $ICC=2.96^2/(2.96^2+2.07^2) = 67\%$. A mayor ICC más relevante es el uso de grupos (RMN) en el modelo.
En la imagen arriba hay nubes de puntos de 6 colores diferentes representando la pertenencia de cada punto a un grupo. La posición de los puntos y la de los centros de las nubes tienen varianza $\sigma_{\epsilon}^2$ y $\sigma_\alpha^2$ respectivamente. La ICC aumenta de izquierda a derecha (20%, 50% y 90%), ilustrando que a mayor ICC mayor es la varianza entre grupos que entre puntos.
Regresión Multinivel Requerida
Intuitivamente, un mayor valor de $\sigma_\alpha$ respecto a $\sigma_{\epsilon}$ corresponde a una mayor relevancia en el uso de grupos, pero ¿A partir de cuál valor son requeridas las RMN? Cuando el índice de efecto del diseño (design effect index) es mayor que $1.1$ se recomienda el uso de RMN [Lai et al. 2015]. Este índice de efecto del diseño (deff) se define como:
\begin{equation} de\textit{ff} = 1+(n_j-1) \cdot ICC \label{eq:deff} \end{equation}
Donde ${n}_j$ es el numero promedio de observaciones por grupo, e ICC la correlación intra-clases. En nuestro ejemplo $de\textit{ff} = 1+(10.3-1) \times 0.67= 7.2$ que justifica el uso de una regresión multinivel con grupos de g.
Si simplificamos la ecuación \eqref{eq:deff}, condicionada a que $de\textit{ff}>1.1$, se encuentra que lo que se requiere es:
$$ \frac{\sigma_{\alpha}}{\sigma_\epsilon} > \frac{1}{\sqrt{10 \cdot n_j-11}} $$
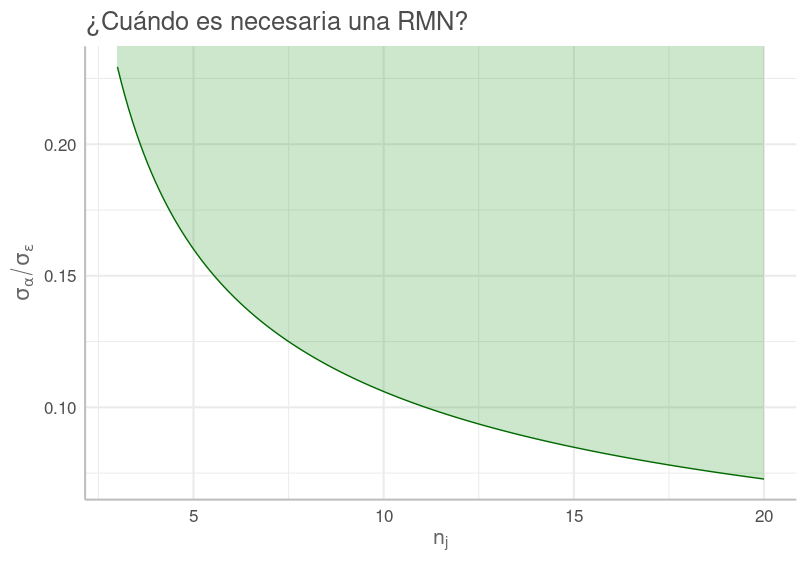
¿Cuándo se requiere una RMN?. Cuando la proporción de $\sigma_\alpha$ entre $\sigma_\epsilon$ está arriba de la curva correspondiente a $\textrm{deff}>1.1$.
Que para $n_j$ entre 5 y 10 requiere que $\sigma_\alpha$ sea mayor que entre 0.16 y 0.11 veces el valor de $\sigma_{\epsilon}$, respectivamente. Lo cual no es una valla muy difícil de pasar.
Toy | Variando Intercepción: Bondad del Ajuste
Hay múltiples y complementarias formas de evaluar la calidad de un modelo ajustado con stan. Aquí veremos un par de ellas para tener idea de cómo progresan nuestros ejemplos.
Chequeo Predictivo de la Posterior
Cada conjunto de parámetros correspondiente a una misma muestra de la posterior de nuestro modelo corresponde a una "solución potencial" del mismo. Con un conjunto de estos parámetros, junto con $X$, podemos replicar los valores de $y$, que denominaremos $\tilde{y}$, prediciendo sus valores según esta solución potencial. Si hacemos estas replicaciones con varias de estas soluciones tomadas al azar de la posterior, obtendremos réplicas $\tilde{y}$ que en conjunto describen tanto la incertidumbre que tenemos de los parámetros, así como la proveniente de la distribución de muestreo en el modelo. A la larga, lo que deberíamos esperar —si nuestro modelo es correcto— es que la distribución de estas réplicas $\tilde{y}$, denominada distribución predictiva (de la) posterior, sea similar a la de la $y$ observada en la data. El chequear cuánto se cumple o no esto se denomina chequeo predictivo (de la) posterior.
La distribución de estas réplicas $\pi(\tilde{y} \mid \tilde{x}, x, y)$ en la notación simplificada es $\pi(\tilde{y} \mid y)$, la cual obtenemos según:
\begin{align} \pi(\tilde{y} \mid y) &= \int \pi(\tilde{y}, \theta \mid y) \, \textrm{d}\theta \nonumber \\ &= \int \pi(\tilde{y} \mid \theta) \cdot \pi(\theta \mid y) \, \textrm{d}\theta \label{eq:posPredFactors} \\ \end{align}
El primer factor en \eqref{eq:posPredFactors} corresponde a la incertidumbre por la distribución de muestreo, y el segundo a la de los parámetros del modelo. En la práctica obtenemos $\tilde{y}$ según lo describimos inicialmente:
\begin{align} \theta^{(m)} \sim p(\theta \mid y) \label{eq:sampleTheta} \\ \tilde{y}^{(m)} \sim p(y \mid \theta^{(m)}) \label{eq:sampleY} \end{align}
En \eqref{eq:sampleTheta} tomamos muestras de $\theta^{(m)}$ de la posterior y en \eqref{eq:sampleY} usamos cada muestra para muestrear a su vez valores de $\tilde{y}^{(m)}$ según su distribución de muestreo. Note cómo estos pasos corresponden a la incertidumbre de los parámetros \eqref{eq:sampleTheta} y de la distribución de muestreo \eqref{eq:sampleY}.
El paquete R bayesplot, desarrollado por el mismo equipo de desarrolladores de stan, incluye decenas de tipos de gráficos para comparar las réplicas $\tilde{y}$ con la data observada $y$ (vea más detalles aquí). Afortunadamente, brms hace fácil acceder a esos gráficos con su función pp_check().
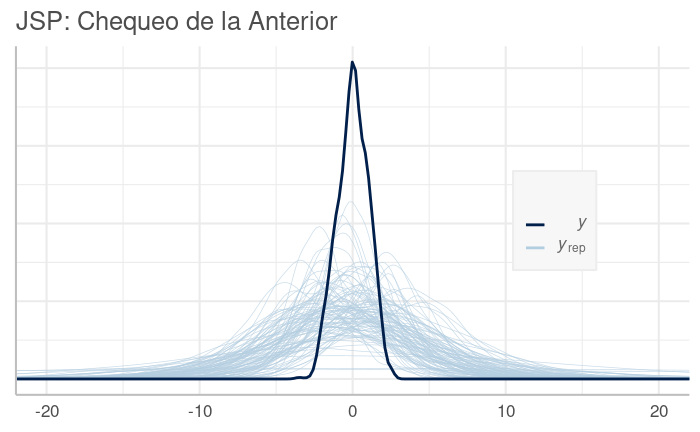
Con la función pp_check() (posterior predictive checking) se obtienen diversos gráficos variando su parámetro type. Por defecto esta función muestra en color celeste la DPP ($y_{rep}$: $y$ replicada) y con azul oscuro la distribución en la data observada $y$.
pp_check(brm2_intc_slo, nsamples=100) +
labs(title="Toy | Variando solo Intercepción y Pendiente por grupo") +
theme(legend.position = c(0.8, 0.5))
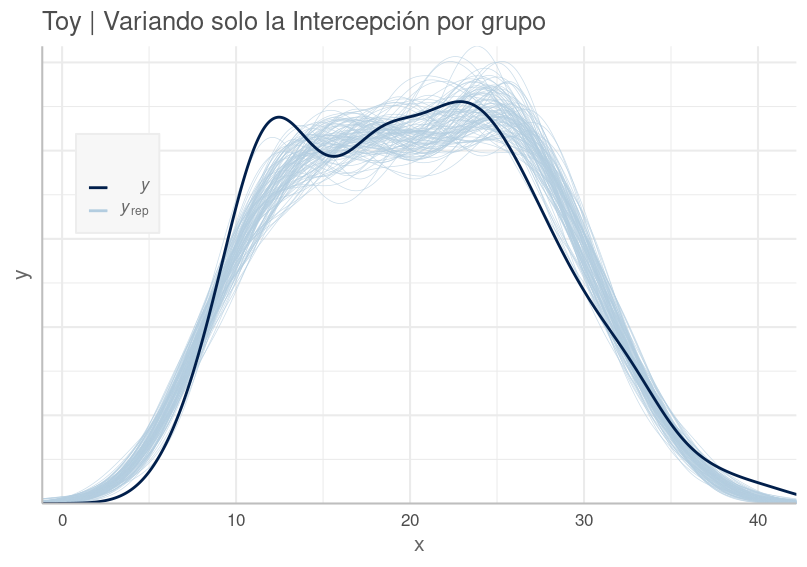
Distribución Predictiva Posterior del Modelo Toy Variando solo Intercepción por Grupo. Nuestro modelo se aproxima, pero no lo suficiente a la data observada.
Si bien no queremos sobre ajustar el modelo a la data, esperamos que siga su patrón general. En el gráfico vemos que nuestro modelo es deficiente en varios tramos, como en las colas.
Criterio de Información Loo
A veces se requiere un índice que cuantifique la bondad del ajuste. En nuestros ejemplos usaremos loo().
loo y WAIC (widely applicable information criterion) son métodos similares —con los mismos supuestos— para estimar la capacidad predictiva fuera-de-la-muestra de un modelo, esto en contraposición a estimaciones de que tan bien el modelo se ajustó a la data, como lo hacen índices del tipo R2.
Se recomienda preferir loo sobre WAIC porque tiene la ventaja de poder darse cuenta cuándo su cálculo ha encontrado dificultades que no hacen confiable su resultado. Esta basado en la verosimilitud de la capacidad predictiva del modelo, calculada usando validación cruzada del tipo deja-uno-afuera (LOO-CV: Leave-one-out cross-validation).
loo(brm2_intc)
Computed from 5000 by 504 log-likelihood matrix
Estimate SE
elpd_loo -1111.3 19.2
p_loo 50.8 4.3
looic 2222.6 38.4
------
Monte Carlo SE of elpd_loo is 0.2.
Pareto k diagnostic values:
Count Pct. Min. n_eff
(-Inf, 0.5] (good) 495 98.2% 533
(0.5, 0.7] (ok) 9 1.8% 103
(0.7, 1] (bad) 0 0.0% <NA>
(1, Inf) (very bad) 0 0.0% <NA>
All Pareto k estimates are ok (k < 0.7).
See help('pareto-k-diagnostic') for details.
El índice loo es reportado de dos maneras (vea más detalles aquí):
elpd_looes un valor que buscamos maximizar (mayor es mejor).looices un valor que buscamos minimizar (menor es mejor).
eplpd_loo es el estimado del logaritmo de la verosimilitud predictiva de $y$ (expected log predictive density) y puede ser positivo o negativo. looic se calcula fácilmente a partir de elpd_loo pues $looic \equiv -2 \times elpd\_loo$.
p_loo es un estimador de la probabilidad de que el modelo prediga valores correctos de $y$ en datos futuros. Asintóticamente —bajo ciertas condiciones— p_loo puede interpretarse como el número efectivo de parámetros. Cuando el modelo tiene un buen comportamiento se observa que $p\_loo < N$ y $p\_loo < p$, donde $p$ es el número total de parámetros en el modelo y $N$ el número de observaciones. Cuando ésto no se cumple, señala que el modelo tiene una capacidad predictiva muy débil y puede indicar un error de especificación grave en el modelo.
Valores de loo() para nuestro modelo
En nuestro modelo, tenemos $p=53$ parámetros (49 intercepciones de grupos + dos coeficientes a nivel población + dos varianzas) y $N=504$, entonces $p\_loo < 53$ y $p\_loo < 504$ por lo que p_loo no es señal de problemas. Los demás estimadores lucen bien respecto a su SE (error estándar) y los usaremos cuando comparemos este modelo con otro. El diagnóstico Pareto muestra que loo ha sido estimado de manera confiable.
Reversión a una Regresión sin Grupos
Las ecuaciones \eqref{eq:rmnIntercF1}-\eqref{eq:rmnIntercF4}, en la notación de de nuestro modelo en \eqref{eq:rmnIntercEx1}, corresponden a
\begin{align} y^{(i)} &= \alpha_0^{(j)} + \beta_0 + {\beta_1}{x}^{(i)} +\epsilon^{(i)} ,~para~j=1, \dots ,J \label{eq:simpToyIntc} \\ \alpha_0^{(j)} &\sim \mathcal{N}(0, \sigma_\alpha^2) \nonumber \\ \epsilon^{(i)} &\sim \mathcal{N}(0, \sigma_{\epsilon}^2) \nonumber \end{align}
En la distribución de $\alpha_0^{(j)}$ podemos ver que conforme $\sigma_\alpha$ se aproxima a cero, entonces $\alpha_0^{(j)}$ se aproxima también a $0$:
$$ \lim_{\sigma_\alpha \to 0} \alpha_0^{(j)} \to 0$$
Es decir, cuando no hay varianza entre grupos, $\alpha_0^{(j)}$ en la ecuación \eqref{eq:simpToyIntc} se vuelve cero, y ésta revierte a
\begin{align*} y^{(i)} &= \beta_0 + {\beta_1}{x}^{(i)} +\epsilon^{(i)} ,~para~j=1, \dots ,J \\ \epsilon^{(i)} &\sim \mathcal{N}(0, \sigma_{\epsilon}^2) \end{align*}
una regresión sin grupos.
Modelo Variando Intercepción y Pendiente
Cuando la intercepción y la pendiente varían por grupos, el modelo aparte de incluir el término $\alpha_1^{(j)} x$ en la parte que cambia por grupo, ahora incluye que $\alpha_0^{(j)}$ y $\alpha_1^{(j)}$ pertenecen a una distribución Normal bivariada con correlación $\rho$. Esta es una extensión natural al caso en el que solo la intercepción varía por grupos, donde $\rho$ no es una restricción adicional, pues claramente puede ser cero.
\begin{align*}
y^{(i)} &= (\alpha_0^{(j)} + \alpha_1^{(j)} x_1) + {X}^{(i)} {\beta} +\epsilon^{(i)} ,~para~i=1, \dots ,N \\
\\
\begin{pmatrix}
\alpha_0^{(j)} \\ \alpha_1^{(j)}
\end{pmatrix}
&\sim
\mathcal{N} \begin{pmatrix}
\begin{pmatrix}
0 \\
0
\end{pmatrix}
,
\begin{pmatrix}
\sigma_{\alpha_0}^2 & \rho~ \sigma_{\alpha_0} \sigma_{\alpha_1} \\
\rho~ \sigma_{\alpha_0} \sigma_{\alpha_1} & \sigma_{\alpha_1}^2
\end{pmatrix}
\end{pmatrix} \label{eq:rmnMulti} \\
\lower 0.4em \epsilon^{(i)} &\sim \mathcal{N}(0, \sigma_{\epsilon}^2)
\end{align*}
Cuando $\beta$ también incluye intercepción y pendiente $\beta_0+\beta_1 x+\cdots$ al igual que los grupos, las estimaciones por grupos están centradas en cero, es decir $\mu_{\alpha_0} = 0$ y $\mu_{\alpha_1} = 0$.
Es importante notar que todos los pares de coeficientes $(\alpha_0^{(j)} , \alpha_1^{(j)})$ provendrán de una misma distribución. Es decir, el modelo "aprende" de toda la data para ajustar la distribución bivariada, y con ésta estima los coeficientes $\alpha_0^{(j)}$ y $\alpha_1^{(j)}$ considerando el patrón de las observaciones en cada grupo.
Es fácil intuir que si tuviéramos variación con otro predictor por grupo como $\alpha_2^{(j)} x_2$, entonces $(\alpha_0, \alpha_1, \alpha_2)$ tendrían un distribución normal tri-variada con una matriz de covarianza de tamaño $3 \times 3$, con 3 coeficientes de correlación: uno para cada par de predictores.
Toy | Variando Intercepción y Pendiente: Ajuste del modelo
Esta vez ajustaremos, a la data Toy, un modelo con intercepción y pendiente variando por grupo. Simplemente modificamos la fórmula para usar x como predictor en las variaciones por grupo: (1 + x | g).
brm2_intc_slo <- brm(y ~ 1 + x + (1 + x | g), data, seed=1234)
summary(brm2_intc_slo)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: y ~ x + (1 + x | g)
Data: data2 (Number of observations: 504)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup samples = 4000
Group-Level Effects:
~g (Number of levels: 49)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 1.31 0.24 0.86 1.82 1.00 1779 2269
sd(x) 0.90 0.11 0.71 1.14 1.00 1974 2983
cor(Intercept,x) 0.14 0.21 -0.26 0.54 1.01 594 1069
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 9.09 0.25 8.60 9.61 1.00 3394 2719
x 3.70 0.14 3.43 3.97 1.00 1391 1860
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 1.55 0.05 1.45 1.66 1.00 4885 3320
Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
El modelo resultante es
\begin{align*}
y^{(i)} &= \alpha_0^{(j)} + \alpha_1^{(j)} + 9.09 + 3.70 x +\epsilon^{(i)} ,~para~i=1, \dots ,504 \\
\begin{pmatrix}
\alpha_0^{(j)} \\ \alpha_1^{(j)}
\end{pmatrix}
&\sim
\mathcal{N}
\begin{pmatrix}
\begin{pmatrix}
0 \\
0
\end{pmatrix}
,
\begin{pmatrix}
1.31^2 & 0.14 \times 1.31 \times 0.90 \\
0.14 \times 1.31 \times 0.90 & 0.90^2
\end{pmatrix}
\end{pmatrix} \\
\epsilon^{(i)} &\sim \mathcal{N}(0, 1.55^2)
\end{align*}
print(coef(brm2_intc_slo), digits = 4)
$g
, , Intercept
Estimate Est.Error Q2.5 Q97.5
1 8.388 0.7567 6.932 9.865
2 8.202 0.5326 7.154 9.215
3 8.440 0.8177 6.828 9.979
:
, , x
Estimate Est.Error Q2.5 Q97.5
1 2.464 0.2915 1.891 3.041
2 3.278 0.1615 2.960 3.598
3 4.377 0.2284 3.934 4.842
:
El error estándar Est.Error de la correlación $\rho$ es más alto que la estimación de la misma, es decir hay incertidumbre de que sea un valor positivo. Lo mismo señala el rango l-95% CI y u-95% CI, con los límites del intervalo creíble de la estimación [Burkner-1], pues contiene el cero.
Este intervalo creíble (bayesiano) es calculado de la distribución posterior de $\rho$ obtenida con stan y es una afirmación de que la probabilidad de que se $\rho$ encuentre en este intervalo es del 95%. En cambio, un intervalo de confianza (frecuentista) de este tipo dice que si obtenemos repetidas muestras, de la misma población de donde proviene la data, y estimamos el intervalo con el mismo método, en el 95% de los casos el intervalo va a contener el parámetro estimado, lo cual no es una afirmación sobre la certidumbre del valor del estimado como ocurre en el modo Bayesiano.
En general, estos intervalos se hacen más angostos con mayor volumen de data y más anchos con la varianza de ésta. En el caso de $\rho$, que por su naturaleza es pequeño, requiere un intervalo muy angosto para ser estadísticamente significativo, el valor verdadero de $\rho$ con el que se generó la data es de $0.4$.
Toy | Variando Intercepción y Pendiente: Bondad del Ajuste
pp_check. Construimos la gráfica de la distribución posterior de $y$ como hicimos antes.
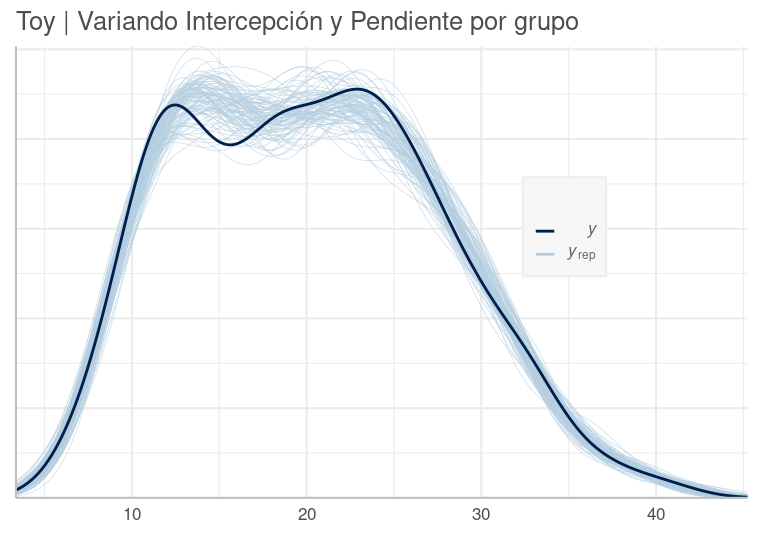
Distribución Predictiva Posterior del Modelo Toy Variando Intercepción y Pendiente por Grupo. El ajuste ahora está mucho mejor explicando el comportamiento observado en la data.
El ajuste ahora está mucho mejor explicando el comportamiento observado en la data.
loo(). El indice loo() que se obtiene ahora es:
Computed from 4000 by 504 log-likelihood matrix
Estimate SE
elpd_loo -977.9 16.3
p_loo 71.3 4.8
looic 1955.8 32.7
------
Monte Carlo SE of elpd_loo is NA.
Pareto k diagnostic values:
Count Pct. Min. n_eff
(-Inf, 0.5] (good) 481 95.4% 502
(0.5, 0.7] (ok) 20 4.0% 100
(0.7, 1] (bad) 3 0.6% 73
(1, Inf) (very bad) 0 0.0% <NA>
See help('pareto-k-diagnostic') for details.
Vemos en Pareto k diagnostic que tenemos tres observaciones con mala clasificación y el estimado de loo podría no ser confiable. Para mayor seguridad, hacemos validación k-fold sobre nuestro último modelo y el anterior, y comparamos los resultados.
brm2_intc_slo <-add_model_metrics(brm2_intc_slo)
brm2_intc_slo_kfold <- kfold(brm2_intc_slo, K=12, chains=5)
brm2_intc_kfold <- kfold(brm2_intc, K=12, chains=5)
compare_ic(brm2_intc_slo_kfold, brm2_intc_kfold)
KFOLDIC SE
brm2_intc_slo 1971.34 33.49
brm2_intc 2237.36 41.54
brm2_intc_slo - brm2_intc -266.02 40.82
Lo cual nos dice que los estimados looic que teníamos eran confiables. De todos modos, en la comparación vemos que este último modelo es definitivamente mejor que el anterior, pues la diferencia es en ese sentido y su magnitud es significativamente diferente que el error estándar de la misma.
Modelo "Verdadero" del Conjunto de Datos Toy
En este anexo encontrará el código usado para generar la data "Toy", donde el modelo implementado es:
$$
\begin{aligned}
y^{(i)} &= \alpha_0^{(j)} + \alpha_1^{(j)} + 2.7 + 1.3 x +\epsilon^{(i)} ,~para~i=1, \dots ,504 \\
\begin{pmatrix}
\alpha_0^{(j)} \\ \alpha_1^{(j)}
\end{pmatrix}
&\sim
\mathcal{N}
\begin{pmatrix}
\begin{pmatrix}
6.2 \\
2.3
\end{pmatrix}
,
\begin{pmatrix}
1.4^2 & 0.4 \times 1.4 \times 0.90 \\
0.4 \times 1.4 \times 0.90 & 0.90^2
\end{pmatrix}
\end{pmatrix} \\
\epsilon^{(i)} &\sim \mathcal{N}(0, 1.6^2)
\end{aligned}
$$
Como ya hemos comentado, al tener el modelo intercepción y pendiente tanto a nivel población como de grupo, la parte del modelo a nivel población ($\beta_0$ y $\beta_1$) obtiene la media de ($\alpha_0$, $\alpha_1$), y a nivel grupo las variaciones centradas en cero.
En nuestra data la media "verdadera" es $\mu_{\alpha_0}=2.7+6.2=8.9$ y $\mu_{\alpha_1}=1.3+2.3=3.6$ mientras que el modelo ha estimado $\beta_0=\mu_{\alpha_0}=9.09$ y $\beta_1=\mu_{\alpha_1}=3.70$, así que considerando las varianzas empleadas estamos razonablemente cerca de los valores "verdaderos".
Note que el modelo de donde proviene la data no es identificable, porque la manera arbitraria como se ha partido la media, de $\alpha_0$ por ejemplo, en $2.7$ para población y $6.2$ por grupos, es una de las infinitas maneras arbitrarias de hacer tal partición y producir la misma data. La respuesta a esto de las RMN, usando la media en la población y variaciones en los grupos, es sencilla y elegante.
Si ajustamos un modelo sin intercepción ni pendiente a nivel de población y ~ -1 + (1 + x | g), deberíamos obtener $\alpha_0^{(j)}$ y $\alpha_1^{(j)}$ centradas en sus medias:
brm2_intc_slo_gr <- brm(y ~ -1 + (1 + x | g), data, seed=1234)
# Media estimada empiricamente de alpha_0
ranef(brm2_intc_slo_gr)$g[,"Estimate","Intercept"] %>% mean()
# Media estimada empiricamente de alpha_1
ranef(brm2_intc_slo_gr)$g[,"Estimate","x"] %>% mean()
[1] 9.128348
[1] 3.707252
Efectivamente, las medias estimadas con el promedio de $\alpha_0^{(j)}$ y $\alpha_1^{(j)}$, cualitativamente coinciden con lo que obtuvimos antes: $9.09$ y $3.70$.
Tipos de Regresiones y de Agrupamiento
Agrupamiento: Completo
$$\begin{aligned}
para~i &= 1, \ldots, N: \\
\bar{y} &= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p
\end{aligned}$$
Una regresión que ignora todo posible agrupamiento, y que por lo tanto considera homogéneos a todos los puntos miembros de una misma población, es denominada de agrupamiento completo. En este caso una única regresión sobre todos los puntos produce una intercepción y pendiente con la tendencia global de las observaciones (línea punteada en el gráfico abajo). Como el modelo no es informado de la tendencia en cada grupo, la regresión representa un sub-ajuste (underfitting) sobre la data: vea grupos 23 y 6 en el gráfico.
Agrupamiento: Ninguno
$$\begin{aligned} para~j &= 1, \ldots, J: \\ \bar{y}^{(j)} &= \beta_0^{(j)} + \beta_1^{(j)} x_1 + \beta_2^{(j)} x_2 + \dots + \beta_p^{(j)} x_p \end{aligned}$$
Una regresión individual sobre cada grupo de puntos, ignorando completamente a los demás, se denomina sin ningún agrupamiento. En este caso se producen tantas intercepciones y pendientes como grupos (con más de un punto) hay en la data (línea de guiones en el gráfico abajo). Como cada regresión solo es informada con el patrón en el grupo, e ignora la tendencia global, tiende a un sobreajuste (overfitting) cuando hay pocas observaciones en el grupo: grupos 12, 22 y 42. Además es incapaz de resolver grupos con solo una observación: grupo 49.
Cuando se hace una regresión con pendiente e intercepción variando por grupo, pero sin usar el modelo Multinivel, (con lm() por ejemplo) se obtienen también estas regresiones sin ningún agrupamiento:
fit <- lm(y ~ 1 + x + g + g:x, data)
Agrupamiento: Parcial
$$\begin{aligned} para~i &= 1, \ldots, N, ~j = 1, \ldots, J: \\ \bar{y}^{(i)} &= \alpha_0^{(j)} + \alpha_1^{(j)} x_1 + \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p \end{aligned}$$
Una regresión Multinivel puede ser entendida como una generalización de los dos tipos de agrupamiento anteriores, en la que se da un agrupamiento parcial. La pendiente e intercepción de cada grupo provienen de una misma distribución, con una media aproximada a la de agrupamiento completo, pero cada coeficiente por grupo es estimado teniendo en cuenta la tendencia de las observaciones en el grupo. Es decir, el modelo es informado tanto por la tendencia global como la local en cada grupo (línea continua en el gráfico abajo).
Cuando hay pocas observaciones, la regresión del grupo tiende al patrón global (grupos 22, 42 y 49), y cuando hay más observaciones la regresión se ajusta más sobre los puntos en el grupo (grupo 23).
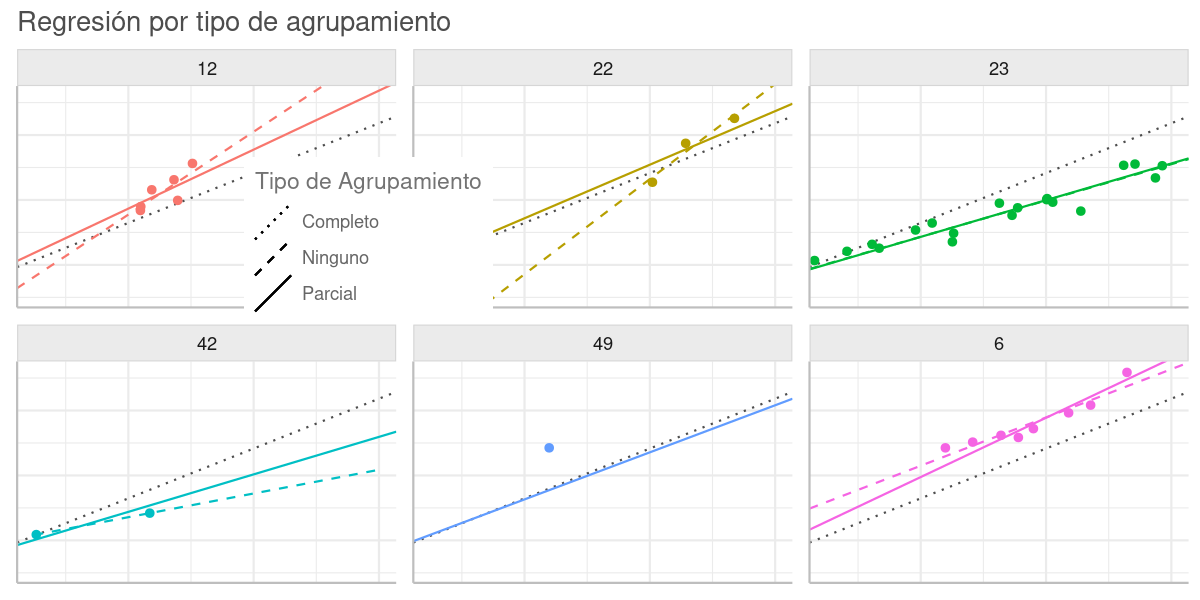
Tipo de Regresión vs Tipo de Agrupamiento.
(A) Agrupamiento: Completo. La línea punteada gris es de una regresión sobre todos los puntos sin grupos. Por ignorar la tendencia de cada grupo, tiende a sub-ajuste (underfitting): grupos 23 y 6.
(B) Agrupamiento: Ninguno. La línea de guiones es de una regresión sobre cada grupo de puntos sin ninguna conexión (agrupamiento) con los demás. Tiende a un sobreajuste (overfitting) cuando hay pocas observaciones en el grupo: grupos 12 y 22. Además es incapaz de resolver grupos con una sola observación: grupo 49.
(C) Agrupamiento: Parcial. La línea continua es de una regresión Multinivel que causa un agrupamiento parcial, donde la pendiente y la intercepción varían entre los dos extremos anteriores. El ajuste sobre los puntos en el grupo es mayor cuando el grupo tiene más observaciones: grupo 23, mientras que es más hacia la tendencia global cuando hay pocos puntos en el grupo: grupos 22, 42 y 49.
Encogimiento en Agrupamiento Parcial
Para ver con más detalle el efecto del agrupamiento parcial en las RMN, compararemos en cada grupo, del modelo Toy, la pendiente obtenida con regresiones usando los tres tipos de agrupamiento que vimos en la sección anterior.
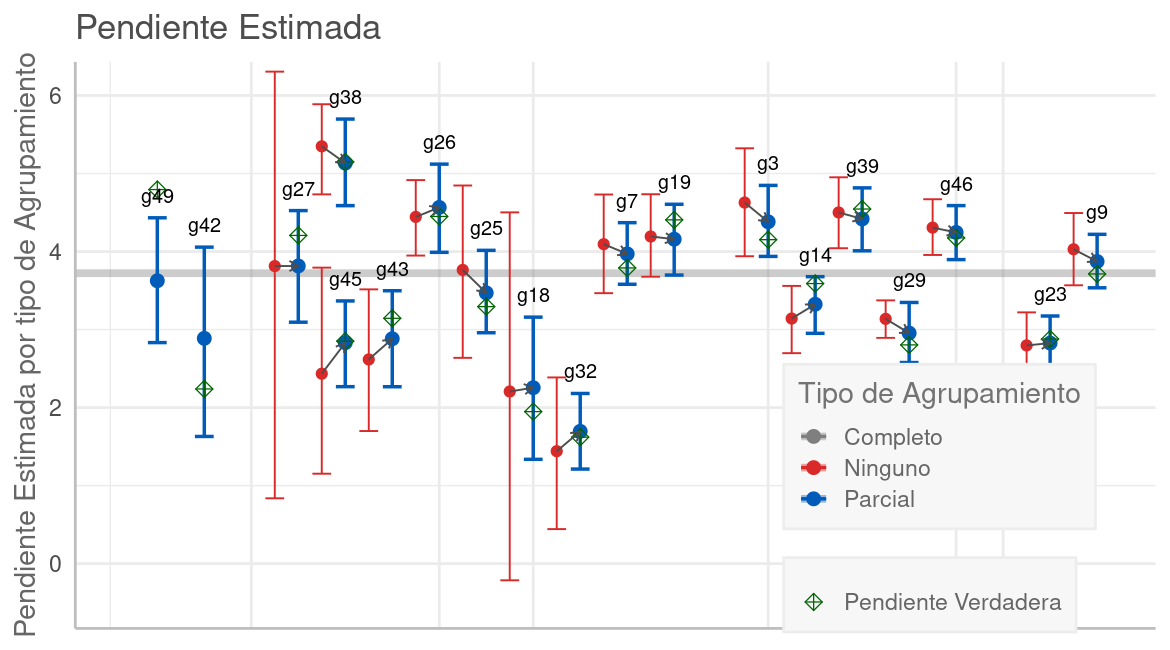
Pendientes por tipo de Agrupamiento. La pendiente de cada grupo está dispuesta a lo largo del eje horizontal de acuerdo con número de observaciones en cada grupo. En la mayoría de los casos las estimaciones Multinivel (punto azul) tienen un valor entre la estimación sin agrupamiento (punto rojo) y la de agrupamiento completo (trazo gris). Esto reduce el ruido en la estimación (intervalos más angostos) y mejora la estimación acercándola más a la pendiente real, que se muestra con un rombo verde.
El trazo horizontal gris grueso es la pendiente de la regresión con agrupamiento total, calculada con stan (inferencia Bayesiana) sobre todas las observaciones. Los puntos representan la pendiente estimada en cada grupo y las líneas verticales su intervalo creíble al 95%. Los grupos están dispuestos en el eje horizontal según su tamaño (número de observaciones), así el grupo 49 -en el extremo izquierdo- tiene una sola observación y el 9 -a la derecha- tiene 21. Como la data es fabricada por nosotros, conocemos el valor "verdadero" de la pendiente, que es mostrado con un rombo verde.
Los trazos en azul son de la regresión Multinivel (calculada con brms) y los de rojo de la regresión sin ningún agrupamiento (una regresión por grupo, calculada con stan). Para el caso de grupos con 3 o menos puntos, stan no pudo calcular la regresión por errores de diagnóstico causados por la escasa data. Es por eso por lo que los dos primeros grupos a la izquierda solo muestran estimaciones en azul de la regresión Multinivel, que sí es capaz de resolver estos casos.
En la mayoría de los grupos, las estimaciones RMN (punto azul) tienen un valor entre la estimación sin agrupamiento (punto rojo) y la de agrupamiento completo (trazo gris), lo cual se denomina encogimiento (shrinkage). Este encogimiento (hacia la media) tiende a ser mayor cuando hay menos observaciones en el grupo, pues la mayor incertidumbre en grupos con pocos puntos es compensada teniendo más en cuenta el patrón global de todos los puntos. Esto se refleja en estimaciones con mayor certidumbre (intervalos más angostos), y en la mayoría de los casos, mejor aproximación al valor verdadero.
Gelman 2013 señala que este encogimiento permite comparar efectos en los grupos sin tener que preocuparse en seguir los procedimientos clásicos de comparaciones múltiples. Incluso propone construir RMNs cuando se requieran estas comparaciones:
Proponemos la construcción de modelos multinivel en los entornos donde surgen múltiples comparaciones. Los modelos multinivel realizan agrupamientos parciales, mientras que los procedimientos clásicos suelen mantener estacionarios los centros de los intervalos, ajustando las comparaciones múltiples haciendo los intervalos más amplios [...]. Por lo tanto, los modelos multinivel abordan el problema de las comparaciones múltiples y también producen estimaciones más eficientes, especialmente en entornos con baja variación a nivel de grupo, que es donde las comparaciones múltiples son una preocupación particular.
Análisis de Datos de "Junior School Project"
Vamos a analizar los datos que Peter Mortimer usó en Un Estudio de Escuelas Primarias Eficaces. Dicho conjunto de datos es conocido como "Junior School Project" (JSP). Los datos estan disponibles en el paquete R faraway con el nombre jsp.
El JSP fue un estudio longitudinal de alrededor de 2000 alumnos de 50 escuelas primarias elegidas al azar de las 636 escuelas de la Inner London Education Authority (ILEA) en 1980. Aquí contamos con un subconjunto de esos datos:
- school: Id de la escuela {1,..., 50} (categórica).
- class: Id del salón {1,..., 4} (categórica).
- student: Id del alumno {1,..., 1402} (categórica).
- gender: Sexo del alumno {m, f} (categórica).
- year: Año de estudio en la escuela primaria {3, 4, 5} (categórica).
- social: Clasificación socioeconómica del padre del alumno (categórica). Los niveles son:
I,II,III nonmanual,III manual,IV,V,lterm unemp(desempleado a largo plazo),curr unemp(actualmente desempleado),father absent(padre ausente). - raven: Puntaje (entre 0 y 40) del alumno en la prueba Raven, que mide el razonamiento abstracto no-verbal. En varios estudios se ha encontrado esta prueba, mediana o altamente correlacionada con el IQ del evaluado. Esta prueba fue evaluada al inicio de los estudios del alumno.
- math: Puntaje (entre 0 y 40) del alumno, por año de estudios, en la prueba de matemáticas.
- english: Puntaje (entre 0 y 100) del alumno, por año de estudios, en la prueba de lenguaje (Inglés).
Objetivo Principal
El objetivo principal del estudio es establecer si algunas escuelas fueron más eficaces que otras para promover el aprendizaje y el desarrollo de los alumnos, después de descontar las diferencias sociodemográficas de los alumnos como gender o raven.
Corrección de Sesgo
Los puntajes de matemáticas y Raven tienen distribuciones con fuerte sesgo (skew) negativo (cola larga a la izquierda) debido a un "efecto de techo" en el que la diferencia de puntaje entre los alumnos más competentes varía muy poco respecto a la habilidad medida. Asimismo, el rango de puntaje en english es diferente al de las otras pruebas. Para corregir estos inconvenientes hemos transformado las variable math, english, y raven usando el paquete R bestNormalize, que analiza varias posibles transformaciones monotónicas (p.ej. Yeo-Johnson, Lambert) y aplica la más eficaz en cada caso. En nuestro caso, el método seleccionado fue Ordered Quantile normalization.
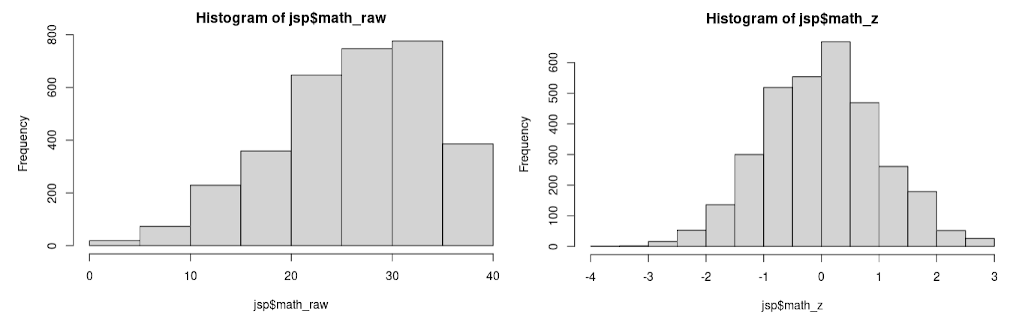
JSP Corrección de Sesgo en los Puntajes. (a) Histograma con los puntajes originales en math, y (b) luego de su normalización.
Esta normalización no parece tan arbitraria si se considera, en primer lugar, que ésta es una práctica que no es rara en instituciones educativas, y en segundo lugar que ellos y nosotros lo hacemos precisamente para corregir el efecto techo encontrado. El efecto techo es señal de que el examen con el que se ha evaluado al alumno no discrimina lo suficiente a los más destacados, y en consecuencia, a partir de cierto nivel de competencia en adelante están recibiendo puntajes similares. Lo ideal es agregar preguntas más difíciles a la prueba para discriminar mejor a los alumnos más competentes, pero en los casos post facto como éste, la normalización redistribuye las notas para corregir esto.
Las variables transformadas han sido además estandarizadas (centradas y escaladas) para tener el cero como media y una desviación estándar como unidad. Estas variables transformadas tienen nombres terminando en _z y los valores originales se conservan en variables que terminan en _raw. El gráfico arriba muestra math_raw (datos originales con el sesgo) y math_z (datos transformados y estandarizados sin sesgo).
str(jsp)
'data.frame': 3236 obs. of 12 variables:
$ school : Factor w/ 49 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
$ student : Factor w/ 1192 levels "1","2","3","4",..: 1 1 1 2 2 3 3 3 4 4 ...
$ year : Factor w/ 3 levels "3","4","5": 1 2 3 1 2 1 2 3 1 2 ...
$ class : Factor w/ 4 levels "1","2","3","4": 1 1 1 1 1 1 1 1 1 1 ...
$ gender : Factor w/ 2 levels "m","f": 2 2 2 1 1 1 1 1 1 1 ...
$ social : Factor w/ 9 levels "I","II","III nonmanual",..: 9 9 9 2 2 2 2 2 9 9 ...
$ raven_z : num -0.403 -0.403 -0.403 -1.588 -1.588 ...
$ math_z : num -0.528 -0.415 -0.528 -1.462 -1.825 ...
$ english_z : num 0.55 0.928 -0.424 -2.128 -1.336 ...
Influencia de la Escuela en el Progreso Académico del Alumno
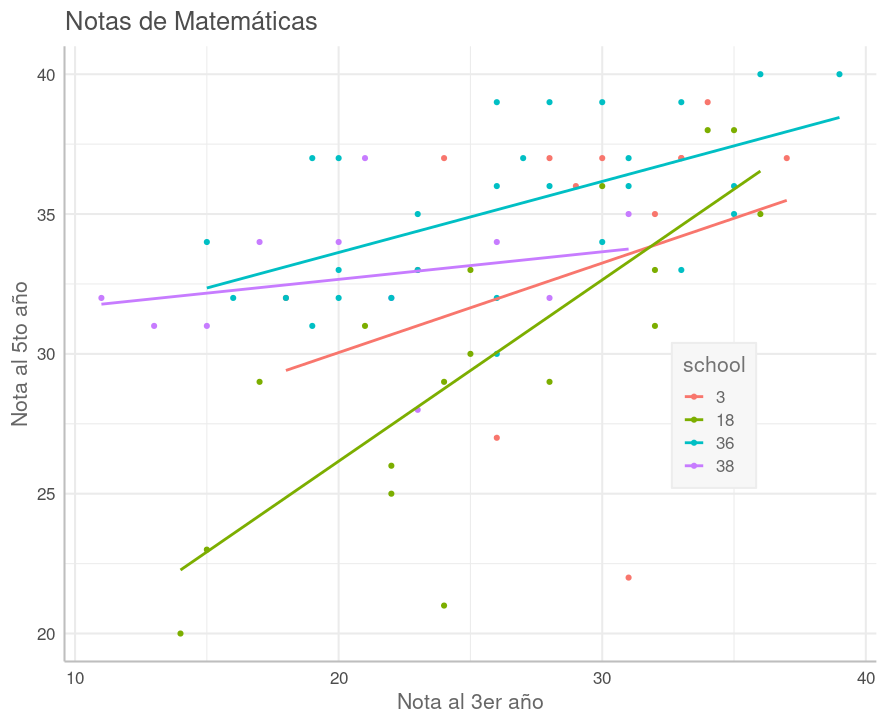
En el gráfico a continuación vemos una comparación entre las notas de matemáticas, al quinto año respecto al tercero, para algunas escuelas seleccionadas. Las líneas corresponden a regresiones lineales clásicas ajustadas sobre las notas de alumnos en una misma escuela, mostrando la tendencia.
En algunas escuelas la regresión es una línea casi paralela, completamente por encima de la de otra escuela (p.ej. 36:celeste sobre 18:verde oliva), que corresponde a que la mayoría de los alumnos en la escuela arriba, progresaron, del 3er al 5to año, más que los alumnos en la escuela abajo. Correspondientemente, la escuela arriba fue más eficaz en la mejora del alumno que la de abajo.
Cuando las líneas de tendencia entre dos escuelas no son paralelas, la que está más arriba en el lado izquierdo corresponde a la que más progreso ha tenido con los alumnos más rezagados, mientras la que está más arriba a la derecha es en la que más han mejorado los alumnos más avanzados. En este sentido, las líneas de poca pendiente corresponden a escuelas donde la brecha entre alumnos rezagados y avanzados ha disminuido.
Como tenemos los puntajes de english y math en el tercer y quinto año podríamos analizar el efecto de la escuela en el rendimiento por materia, pero terminaríamos con dos modelos y dos clasificaciones de las escuelas (una por cada materia). Aun cuando podríamos ver la manera de consolidar esos resultados en una sola clasificación, ésta parece una ruta complicada.
Fusionar Materias
Como hemos normalizado las notas de ambas materias, aquí hemos elegido unirlas y considerarlas simplemente puntajes al tercer score_3_z y quinto año score_5_z. Esto nos ayuda a mostrar el uso de RMN sin complicarnos en exceso con el análisis. Asimismo, siguiendo el mismo criterio, hemos conservado solo los alumnos que han estudiado del 3ro al 5to año en una misma escuela.
str(jsp_sc)
tibble [1,774 × 13] (S3: tbl_df/tbl/data.frame)
$ school : Factor w/ 49 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
$ student : Factor w/ 1192 levels "1","2","3","4",..: 1 3 4 6 7 8 11 14 15 16 ...
$ class : Factor w/ 4 levels "1","2","3","4": 1 1 1 1 1 1 1 1 1 1 ...
$ gender : Factor w/ 2 levels "m","f": 2 1 1 2 1 2 2 2 2 1 ...
$ social : Factor w/ 9 levels "I","II","III nonmanual",..: 9 2 9 4 9 9 4 2 7 5 ...
$ raven_z : num [1:1774] -0.403 -0.576 -1.817 -1.401 -1.256 ...
$ score_3_z : num [1:1774] -0.351 1.655 -0.215 -0.873 -0.485 ...
$ score_5_z : num [1:1774] -1.07056 1.83063 -0.00526 -2.20746 -0.78523 ...
Desde esta perspectiva, la variable dependiente "$y$" es score_5_z, y las variables predictoras son score_3_z, raven_z, school, gender, y social. Como es usual, la intercepción en la regresión tendrá las unidades de $y$, que debido al escalado que hicimos, es una desviación estándar de score_5_z, a la que para abreviar llamaremos $\sigma_y$. La intercepción corresponde al caso cuando score_3_z=0 y raven_z=0, que debido al centrado de estas variables, es el puntaje esperado en 5to año cuando el alumno ha obtenido el puntaje promedio en score_3_z y raven_z, es decir la intercepción es el puntaje del alumno promedio.
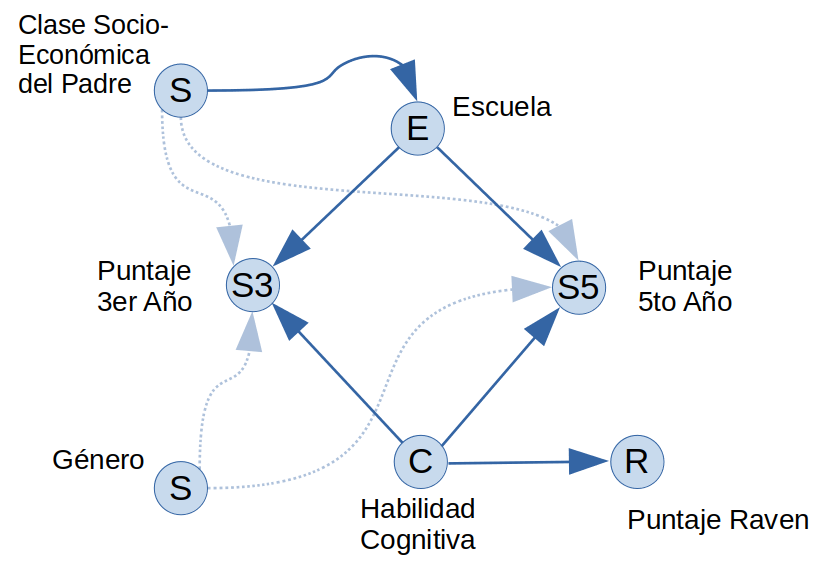
Diagrama Causal
La hipótesis principal del estudio es que la escuela influye en cuanto aprende el alumno, lo cual se refleja en la mejora de su puntaje de 3ro a 5to año, es decir $\text{(score_5_z - score_3_z)} \sim \text{school} + \text{otros}$ donde $\sim$ significa "depende de". Por lo tanto, $\text{score_5_z} \sim \text{score_3_z} + \text{school} + \text{otros}$.
EL diagrama causal arriba considera que la escuela y la habilidad cognitiva del alumno influyen en sus notas, donde dicha habilidad cognitiva es una variable no observada pero estimada con el puntaje en la prueba Raven.
En varias escuelas, la cantidad de alumnos con padres en las diferentes clasificaciones sociales está bastante desbalanceada hacia las clases más altas o las más bajas, por lo que parece posible que la clase social del padre influya en la selección de la escuela en la que estudia el alumno. También es posible que esta clase del padre influya en el entorno y las facilidades que tiene para estudiar y en consecuencia influya en sus notas, lo cual se muestra con líneas tenues.
Finalmente, el género del alumno podría tener algún rol en el desempeño del alumno lo cual se muestra también con líneas tenues.
Modelo de Referencia
Para tener una noción del progreso en los siguientes modelos, vamos a construir el modelo más simple posible, en el que las notas de 5to año son constantes.
$$\begin{aligned} y^{(i)} &\equiv \textrm{score_5_z}^{(i)} = \beta_0 + \sigma_\epsilon^{(i)} \\ \epsilon^{(i)} &\sim \mathcal{N}(0, \sigma_{\epsilon}^2) \end{aligned}$$
jsp_null <- brm(score_5_z ~ 1, data=jsp_sc)
jsp_null
loo(jsp_null)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: score_5_z ~ 1
Data: jsp_sc (Number of observations: 1774)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup samples = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 0.00 0.02 -0.05 0.05 1.00 3520 2341
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 1.00 0.02 0.97 1.03 1.00 3591 2725
Computed from 4000 by 1774 log-likelihood matrix
Estimate SE
elpd_loo -2518.7 27.2
p_loo 1.9 0.1
looic 5037.4 54.4
------
Monte Carlo SE of elpd_loo is 0.0.
All Pareto k estimates are good (k < 0.5).
La intercepción $\beta_0=0.00$ es la media de $y \equiv \textrm{score_5_z}$, que es cero por efecto de su centrado. Recordemos que $\sigma_{\epsilon}$, representado por sigma en el listado arriba, tiene las mismas unidades que $y$. Entonces, como sigma=1.00, hay una desviación estándar $\sigma_{\epsilon}=1.00 \times \sigma_y$ en las notas de 5to año que no son explicadas por el modelo.
Intercepción por Escuela y por Categoría Social
Para evaluar si es apropiado usar grupos por escuela school y por clasificación social del padre social en nuestro modelo, lo ajustaremos a la data solo solo con intercepciones en estos grupos y con los predictores a nivel población que usaremos en nuestro modelo final.
jsp_m0 <- brm(score_5_z ~ gender + score_3_z + raven_z + (1 | school) + (1 | social),
data=jsp_sc, refresh=0)
There were 127 divergent transitions after warmup.
The largest R-hat is 1.06, indicating chains have not mixed.
Effective Samples Size (ESS) is too low, indicating posterior means and medians
and tail quantiles may be unreliable.
stan tiene dificultad para muestrear la posterior, esto se refleja en divergencias después del calentamiento (lea acerca de eso aquí). En nuestro caso se requieren más iteraciones iter=3000 y más calentamiento warmup=2000 (por defecto son 2000 y 1000 respectivamente), y hace falta un mayor valor para los parámetros adapt_delta=0.999 y max_treedepth=12 (por defecto son $0.8$ y $10$ respectivamente), use el vínculo sugerido anteriormente para entender mejor qué controlan estos parámetros.
jsp_m0 <- brm(
score_5_z ~ gender + score_3_z + raven_z + (1 | school) + (1 | social),
data = jsp_sc,
seed = 123,
iter = 3000, warmup = 2000,
control = list(adapt_delta = 0.99, max_treedepth = 12)
)
jsp_m0 <- add_criterion(jsp_m0, "loo")
jsp_m0
loo(jsp_m0)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: score_5_z ~ gender + score_3_z + raven_z + (1 | school) + (1 | social)
Data: jsp_sc (Number of observations: 1774)
Samples: 4 chains, each with iter = 3000; warmup = 2000; thin = 1;
total post-warmup samples = 4000
Group-Level Effects:
~school (Number of levels: 48)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.24 0.03 0.19 0.31 1.00 1268 2030
~social (Number of levels: 9)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.08 0.04 0.02 0.19 1.01 796 822
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept -0.01 0.05 -0.12 0.09 1.00 1188 1977
genderf 0.04 0.03 -0.02 0.10 1.00 6771 3002
score_3_z 0.62 0.02 0.59 0.66 1.00 4194 3061
raven_z 0.17 0.02 0.13 0.21 1.00 4040 2532
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 0.62 0.01 0.60 0.64 1.00 6589 2717
Estas intercepciones por grupo son el efecto medio de las escuelas y la clase social en la nota de 5to año, con $\sigma_y$ como unidad. La intercepción a nivel población corresponde a la de los hombres, y genderf es la intercepción para las mujeres, donde la alumna promedio tiene $0.05\,\sigma_y$ mejor puntaje que el alumno promedio.
La varianza entre escuelas es $0.24^2$, y entre categorías sociales es $0.08^2$ que corresponden a un $ICC=0.24^2/(0.62^2+0.24^2+0.08^2)=12.8\%$ y $1.4\%$ respectivamente. Adicionalmente, la cantidad promedio de observaciones por escuela es $37$ y por categoría social es $197$, por lo que para las escuelas tenemos $\textit{deff}=1+(37-1)\times 0.128=5.6>1.1$ y para social $\textit{deff}=1+(197-1)\times 0.014=3.74>1.1$ por lo que es necesario mantener el modelando de la data con esos dos grupos.
El efecto de las escuelas $\sigma_{school}=0.24$ es grande. Si comparamos una escuela en el $5\%$ superior $+1.6\,\sigma$ con una en el $5\%$ inferior $-1.6\,\sigma$ estamos hablando de una diferencia de $2 \times 1.6 \times 0.24\,\sigma_y=0.77\, \sigma_y$. Es decir, la nota del alumno promedio en una muy buena escuela está $0.77 \sigma_y$ por encima de la del mismo alumno en una escuela muy mala. Para poner esto en perspectiva, esta diferencia corresponde a $\text{score_3_z} = 0.97$ más $\text{raven_z} = 0.97$, pues $0.97 \times 0.62\,\sigma_y + 0.97 \times 0.17\sigma_y = 0.77\, \sigma_y$. Es decir, en este modelo, el alumno en una muy mala escuela necesita tener un
score_3_zyraven_zcasi con una desviación estándar sobre el promedio para alcanzar al alumno promedio en una muy buena escuela.
Hacia el Modelo Final
formula <- score_5_z ~ 1 + gender + score_3_z + raven_z +
(1 + score_3_z + raven_z | school) + (1 + score_3_z + raven_z | social)
Exploratoriamente, nuestro modelo final propone que el puntaje al quinto año score_5_z, depende del género del alumno gender, y de su habilidad de razonamiento raven, pues esto ayuda a su aprendizaje. Además, propone que estas variables predictoras tienen influencia diferente en el alumno dependiendo de la escuela (*|school) y de la clasificación socioeconómica del padre (*|social).
En este caso gender es una variable categórica a nivel población. No es una buena idea crear un grupo con esta variable pues tiene apenas dos valores posibles y técnicamente no es posible encontrar la varianza entre solo dos valores con un nivel de certeza razonable. Por otro lado, al tener nuestro modelo tanto intercepción como variables categóricas a nivel población, vamos a obtener la intercepción global y solo la intercepción para uno de los géneros (como vemos [en el modelo anterior(#jspIntcOnly)]). Esto ocurre porque no es identificable tener una intercepción global más una por cada género. De manera que vamos a remover la intercepción global para poder obtener la de cada género.
formula <- score_5_z ~ 0 + gender + score_3_z + raven_z +
(1 + score_3_z + raven_z | school) + (1 + score_3_z + raven_z | social)
Asignación de Distribuciones Anteriores
Esta vez vamos a establecer nosotros algunas distribuciones anteriores (priors) del modelo, en vez de usar las asignaciones por defecto como hemos venido haciendo. Para ver las distribuciones anteriores del modelo podemos usar la función get_prior.
(jsp_priors <- get_prior(formula, jsp_sc))
prior class coef group resp dpar nlpar bound
1 b
2 b genderf
3 b genderm
4 b raven_z
5 b score_3_z
6 lkj(1) cor
7 cor school
8 cor social
9 student_t(3, 0, 2.5) sd
10 sd school
11 sd Intercept school
12 sd raven_z school
13 sd score_3_z school
14 sd social
15 sd Intercept social
16 sd raven_z social
17 sd score_3_z social
18 student_t(3, 0, 2.5) sigma
En este artículo encontrará sugerencias para estas distribuciones anteriores. En el listado arriba vemos que como hemos omitido la intercepción global, vamos a obtener los coeficientes genderf y genderm, correspondientes a la intercepción de cada género, tal como queríamos.
Los parámetros con la columna prior en blanco tienen una distribución anterior asignada por defecto por stan, y las que no están en blanco son las asignadas por defecto por brms. Es posible establecer una distribución anterior para cada parámetro por separado, o puede establecerse una misma distribución para un subconjunto de estos, como lo denotan las filas 1, 6, y 9. Así —por ejemplo— se puede apreciar que los priors con class=b son asignados por stan (están en blanco), mientras que los de las clases class=cor, class=sd y class=sigma tienen distribuciones por defecto de brm (filas 6, 9, 18). Más precisamente, la fila 6 indica que el prior con class=cor (la correlación entre coeficientes de un mismo grupo), para ambos grupos es lkj(1) (LKJ).
La class=b corresponde a la distribución anterior de los coeficientes a nivel de población. Como nuestras variables estan estandarizadas, a esos coeficientes vamos a darles la distribución $\mathcal{N}(0,2)$.
jsp_priors[1, 1] <- prior(normal(0, 2))
Recordemos que el modelo va a estimar un juego de coeficientes para los predictores (incluyendo la intercepción) para cada miembro de un grupo, pero todos los coeficientes de un mismo grupo provienen de una misma distribución normal multivariada. Como nuestro modelo incluye dos grupos, tenemos dos distribuciones multivariadas.
Las anteriores con la clase sd y con la columna group no en blanco, corresponden a la desviación estándar de los predictores en cada grupo, como $\sigma_{\alpha_0}$ y $\sigma_{\alpha_1}$ en $\eqref{eq:rmnMulti}$. Para estos vamos a usar una distribución Exponencial(1).
jsp_priors[9, 1] <- prior(exponential(1))
La class=sigma corresponde a la desviación estándar a nivel de población $\sigma_{\epsilon}$. Ya hemos visto que ésta es menor que 1, así que vamos a asignarle una distribución Cauchy(0, 1).
jsp_priors[18, 1] <- prior(cauchy(0, 0.8))
Finalmente, hay que notar que como una desviación estándar solo pueden tener valores positivos, cuando le asignamos una distribución con posibles valores negativos, como la Normal o Cauchy, internamente brm hace el ajuste del caso para que solo se use la parte positiva (truncada) de dicha distribución.
Chequeo Predictivo de la Distribución Anterior
Podemos revisar la bondad de nuestras distribuciones anteriores calculando directamente sus predicciones. Es decir, muestreamos parámetros de la distribución anterior y los introducimos en la fórmula del modelo (junto con los predictores en la data) para obtener $\tilde{y}_{\textrm{rep}}$ de la distribución de muestreo. Esto es análogo al Chequeo Predictivo de la Posterior que hicimos antes, solo que en lugar de usar la distribución de los parámetros condicionados a la data usamos sus anteriores (distribuciones no condicionadas a la data).
Podemos hacer esto facilmente con brm() usando el parámetro sample_prior = "only"; luego graficamos la distribución de los valores predecidos $y_{rep}$ la compararemos con el de la data usando pp_check().
jsp_m1_prior <- brm(
formula,
data = jsp_sc,
seed = 123,
prior = jsp_priors,
sample_prior = "only",
iter = 1200, warmup = 200, refresh = 0
)
pp_check(jsp_m1_prior, nsamples = 70) +
labs(title="JSP: Chequeo de priors") +
theme(legend.position = c(0.8, 0.5)) +
coord_cartesian(xlim=c(-20,20))
Lo que deseamos encontrar es que la $y_{rep}$ de los anteriores tenga una distribución aproximadamente proporcional a la de $y$ observada, pero dando posibilidad a un rango razonablemente más amplio de valores.
Las predicciones de nuestras distribuciones anteriores se ven bien ✅.
Ajuste del Modelo a la Data
Habiendo confirmado que nuestras distribuciones anteriores son razonables, ajustamos el modelo a la data.
jsp_m1 <- brm(
formula,
data = jsp_sc,
seed = 123,
prior = jsp_priors,
iter = 2500, warmup = 1500,
control = list(adapt_delta = 0.99)
)
jsp_m1 <- add_criterion(jsp_m1, "loo")
Family: gaussian
Links: mu = identity; sigma = identity
Formula: score_5_z ~ 0 + gender + score_3_z + raven_z +
(1 + score_3_z + raven_z | school) + (1 + score_3_z + raven_z | social)
Data: jsp_sc (Number of observations: 1774)
Samples: 4 chains, each with iter = 2500; warmup = 1500; thin = 1;
total post-warmup samples = 4000
Group-Level Effects:
~school (Number of levels: 48)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.25 0.03 0.19 0.31 1.00 1297 2224
sd(score_3_z) 0.11 0.02 0.07 0.16 1.00 1924 2935
sd(raven_z) 0.04 0.03 0.00 0.09 1.00 1262 1960
cor(Intercept,score_3_z) -0.75 0.15 -0.96 -0.41 1.00 1566 2115
cor(Intercept,raven_z) 0.16 0.42 -0.71 0.89 1.00 4144 2621
cor(score_3_z,raven_z) -0.24 0.45 -0.90 0.73 1.00 3282 3136
~social (Number of levels: 9)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.08 0.04 0.01 0.18 1.00 1013 975
sd(score_3_z) 0.03 0.02 0.00 0.08 1.00 2548 2027
sd(raven_z) 0.06 0.04 0.00 0.16 1.00 1167 1548
cor(Intercept,score_3_z) 0.01 0.49 -0.87 0.87 1.00 4384 2707
cor(Intercept,raven_z) -0.07 0.46 -0.88 0.79 1.00 2604 2395
cor(score_3_z,raven_z) -0.12 0.49 -0.92 0.81 1.00 1797 2993
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
genderm -0.01 0.05 -0.12 0.09 1.00 1145 1799
genderf 0.03 0.05 -0.07 0.14 1.00 1058 1673
score_3_z 0.62 0.03 0.56 0.68 1.00 2056 2236
raven_z 0.17 0.03 0.10 0.23 1.00 2341 1971
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 0.61 0.01 0.59 0.63 1.00 6454 2912
La varianza de raven_z entre escuelas y de score_3_z entre clasificaciones sociales parece demasiado pequeña. Probemos sin esos predictores en dichos grupos.
jsp_m2 <- update(
jsp_m1,
formula= score_5_z ~ 0 + gender + score_3_z + raven_z +
(1 + score_3_z | school) + (1 + raven_z | social)
)
jsp_m2 <- add_criterion(jsp_m2, "loo")
loo(jsp_m2, jsp_m1)
:
Model comparisons:
elpd_diff se_diff
jsp_m2 0.0 0.0
jsp_m1 -1.2 0.9
La diferencia entre el anterior modelo jsp_m1 y este último jsp_m2 no es significativa, pues la magnitud de la diferencia de $\text{elpd_loo}$ entre ellos "$\text{elpd_diff}=-1.2$" además de ser muy pequeña, apenas es $1.2/0.9=1.3$ veces mayor que su diferencia estándar, por lo que nos quedamos con el más simple: el último.
Modelo Final
Nuestro modelo final, incluyendo las distribuciones anteriores, es:
\begin{align}
\text{--- A nivel Alumno:}
\nonumber \\
\text{score_5_z} &= \beta_0^{(gender)}
+ \beta_1 \, \text{raven_z}
+ \beta_2 \, \text{score_3_z}
+ \pmb{\alpha}^{(school)}
+ \pmb{\gamma}^{(social)}
+ \epsilon \label{eq:jspFinal}
\\
\text{prior:} \nonumber \\
\epsilon &\sim \mathrm{Cauchy}(0, 1)
\nonumber \\[0.8em]
\text{--- A nivel Escuela:}
\nonumber \\
\pmb{\alpha}^{(school)} &= \alpha_0^{(school)}
+ \alpha_1^{(school)} \, \text{score_3_z} \label{eq:jspSchool}
\\
\begin{pmatrix}
\alpha_0^{(school)} \ \alpha_1^{(school)}
\end{pmatrix}
&\sim
\mathcal{N}
\begin{pmatrix}
\begin{pmatrix}
0 \
0
\end{pmatrix}
,
\Sigma_{school}
\end{pmatrix}
\nonumber \\
\text{priors:} \nonumber \\
\Sigma_{school} &= \operatorname{diag}(\boldsymbol{\mathbf{\tau}}_\alpha) \, \boldsymbol{\mathbf{\Omega}}_\alpha \operatorname{diag}(\boldsymbol{\mathbf{\tau}}_\alpha)
\nonumber \\
\boldsymbol{\mathbf{\tau}}_\alpha^{(j)} &\sim \mathrm{Exponential}(1), \; j = 1, 2 \
\nonumber \\
\boldsymbol{\mathbf{\Omega}}_\alpha &\sim \mathrm{LKJ}(1)
\nonumber \\[1em]
\text{--- A nivel Clase Social del Padre:}
\nonumber \\
\pmb{\gamma}^{(social)} &= \gamma_0^{(social)}
+ \gamma_1^{(social)} \, \text{raven_z} \label{eq:jspSocial}
\\
\begin{pmatrix}
\gamma_0^{(social)} \ \gamma_1^{(social)}
\end{pmatrix}
&\sim
\mathcal{N}
\begin{pmatrix}
\begin{pmatrix}
0 \
0
\end{pmatrix}
,
\Sigma_{social}
\end{pmatrix}
\nonumber \\
\text{priors:} \nonumber \\
\Sigma_{social} &= \operatorname{diag}(\boldsymbol{\mathbf{\tau}}_\gamma) \, \boldsymbol{\mathbf{\Omega}}_\gamma \operatorname{diag}(\boldsymbol{\mathbf{\tau}}_\gamma)
\nonumber \\
\boldsymbol{\mathbf{\tau}}_\gamma^{(j)} &\sim \mathrm{Exponential}(1), \; j = 1, 2 \
\nonumber \\
\boldsymbol{\mathbf{\Omega}}_\gamma &\sim \mathrm{LKJ}(1) \nonumber
\end{align}
jsp_m2
loo(jsp_m2)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: score_5_z ~ gender + score_3_z + raven_z + (1 + score_3_z | school) + (1 + raven_z | social) - 1
Data: jsp_sc (Number of observations: 1774)
Samples: 4 chains, each with iter = 2500; warmup = 1500; thin = 1;
total post-warmup samples = 4000
Group-Level Effects:
~school (Number of levels: 48)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.24 0.03 0.19 0.31 1.00 1103 2138
sd(score_3_z) 0.10 0.02 0.06 0.15 1.00 1444 2434
cor(Intercept,score_3_z) -0.79 0.14 -0.99 -0.44 1.00 1512 2347
~social (Number of levels: 9)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.08 0.04 0.02 0.18 1.00 1071 854
sd(raven_z) 0.06 0.04 0.00 0.15 1.01 967 1664
cor(Intercept,raven_z) -0.05 0.51 -0.92 0.85 1.00 2056 2278
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
genderm -0.01 0.06 -0.11 0.11 1.00 903 1899
genderf 0.03 0.05 -0.07 0.14 1.00 902 1794
score_3_z 0.62 0.03 0.57 0.67 1.00 1252 2679
raven_z 0.17 0.03 0.11 0.23 1.00 2421 2523
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 0.61 0.01 0.59 0.63 1.00 6072 2520
Computed from 4000 by 1774 log-likelihood matrix
Estimate SE
elpd_loo -1671.5 33.6
p_loo 66.3 3.1
looic 3342.9 67.2
------
Monte Carlo SE of elpd_loo is 0.1.
All Pareto k estimates are ok (k < 0.7).
Nuestro modelo final explica el $1-0.61^2/1.00^2=63\%$ de la varianza de las notas de 5to año score_5_z ✅. Asimismo, $loo$ ha mejorado notoriamente.
Interpretación Preliminar
Una nota que debemos poner junto a cada interpretación que hagamos de los parámetros del modelo es (*) "... en un modelo de regresión de las notas en primaria descontando el efecto de la escuela, el género, la categoría social del padre, y la capacidad de razonamiento abstracto del alumno."
La intercepción a nivel población, que es parte de la nota esperada del alumno promedio, está separada por género (genderm:masculino, genderf:femenino) y es muy pequeña, aunque con una ligera ventaja de las chicas sobre los chicos.
A nivel de escuelas, hay una correlación negativa $-0.79$ entre la intercepción y la pendiente de score_3_z, es decir a mayor intercepción menor pendiente y viceversa.
A nivel población, el coeficiente para raven_z es la correlación entre el puntaje en dicha prueba y la nota de 5to año, descontando las demás variables en el modelo, con un valor estimado en $17\%$. El coeficiente para score_3_z tiene una interpretación análoga, con un estimado en $62\%$. Si calculamos la correlación bruta entre score_3_z y score_5_z obtenemos $73\%$ Si consideramos nuestro [Diagrama Causal(#causalNet)], esto sugiere que $73\%-62\%=11\%$ proviene del efecto de las otras variables predictoras en dichas notas.
Chequeo de la Posterior
Demos una mirada a un par de chequeos gráficos para tener una intuición de que tan bien está el modelo.
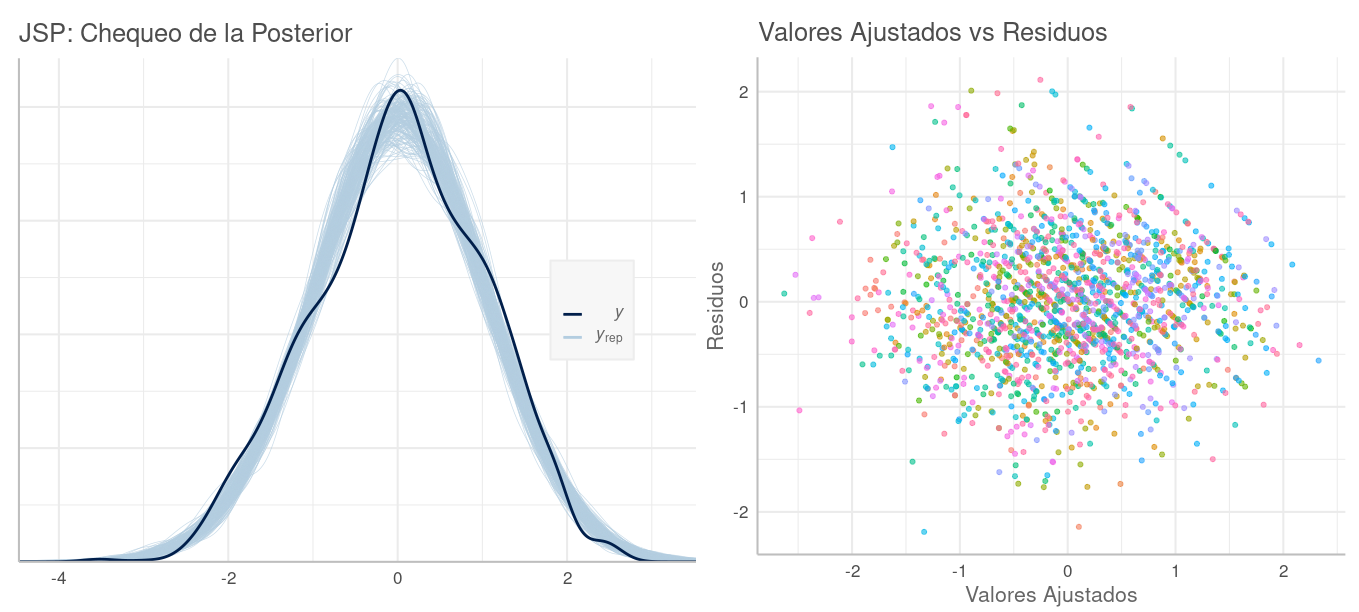
JSP: Chequeo del Modelo Final. (a) Chequeo Predictivo Posterior del modelo, que luce bien. (b) Chequeo de Residuos vs Valores Ajustados ($\tilde{y}$ predicha), donde no hay patrones en la distribución de los puntos ni en su variabilidad. Los patrones diagonales son artefactos debido a que la data original es discreta.
El modelo luce bien en ambos graficos. En el primer gráfico vemos que la distribución de las predicciones del modelo contiene a la data observada. Aun cuando hay segmentos donde la data observada ésta en el margen de las predicciones, no se aleja demasiado. En el segundo no hay patrón en los residuos ni cambio en su variabilidad. Los patrones diagonales son artefactos causados por la data que es discreta.
Una Regresión por Alumno
Como los puntajes están conformados por las notas en math e english, podemos trazar para cada alumno una línea uniendo las notas en esas dos materias.
step <- 0.05
sel_school <- c(29, 22, 1, 14, 41, 38, 36, 31)
subset <- jsp_sc %>% filter(school %in% sel_school)
subset <- subset %>%
mutate(fake = F) %>%
bind_rows(
subset %>% mutate(score_3_z = score_3_z - step, fake = T),
subset %>% mutate(score_3_z = score_3_z + step, fake = T)
) %>% arrange(student, score_3_z)
preds <- posterior_predict(jsp_m2, subset) %>% colMeans()
subset <- subset %>% mutate(pred = preds)
subset %>%
ggplot(aes(x = score_3_z, color = school)) +
geom_point(
data = . %>% filter(fake == F), alpha=0.6,
aes(y = score_5_z)
) +
geom_line(
aes(y = pred, group = student, color = school)
) +
labs(
title = "Puntajes de Escuelas Seleccionadas",
x = "Puntaje al 3er año", y = "Puntaje al 5to año"
) +
theme(legend.position=c(0.9,0.35))
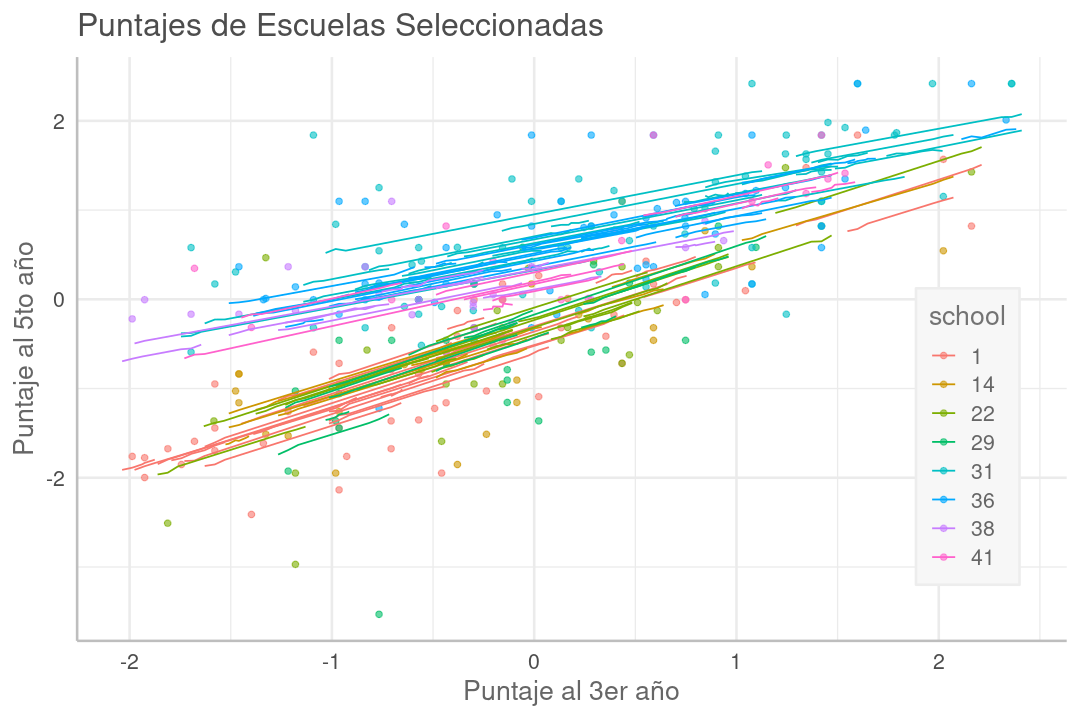
JSP: Predicciones en escuelas seleccionadas. Se incluye solo las ocho escuelas con las intercepciones más altas y las más bajas. Segmentos de línea unen las predicciones de las notas para inglés y matemáticas de cada alumno. Estas líneas convergen en la esquina superior derecha del gráfico correspondiendo a que los alumnos más destacados obtienen puntajes elevados dependiendo menos de la escuela en la que estudian, en oposición a los alumnos más rezagados (en el extremo inferior izquierdo) que obtienen notas más diferentes dependiendo de la escuela.
En el gráfico "JSP: Predicciones en escuelas seleccionadas" arriba cada línea corresponde a un alumno, la línea une sus notas en 3er año con las de 5to, y se incluyen solo las ocho escuelas con las intercepciones más altas o bajas. Estas líneas convergen aproximadamente en la esquina superior derecha del gráfico. Esto corresponde a una correlación negativa, estimada en $\text{cor(Intercept,\, score_3_z)}=-0.79$ entre la intercepción y pendiente por escuela, cuya interpretación es:
Los alumnos más destacados obtienen puntajes elevados variando menos con la escuela en la que estudian, en oposición a los alumnos más rezagados cuyas notas varían más con la escuela. Cuando la escuela tiene un efecto negativo en el alumno (respecto al efecto medio de las escuelas), el impacto es mayor en los alumnos más rezagados.
Hipótesis= Proposición con Parámetros Estimados
A partir de la distribución conjunta de los parámetros del modelo podemos probar diferentes hipótesis de una manera que es imposible con estimaciones puntuales clásicas. Con hipótesis nos referimos a una proposición que depende de uno o más parámetros estimados por el modelo, como por ejemplo "$\beta_0>0$" o "$\alpha_0^{(2)}> \alpha_0^{(3)}$". A continuación, veremos algunos ejemplos.
Ejemplo Comparando la Intercepción de dos Escuelas
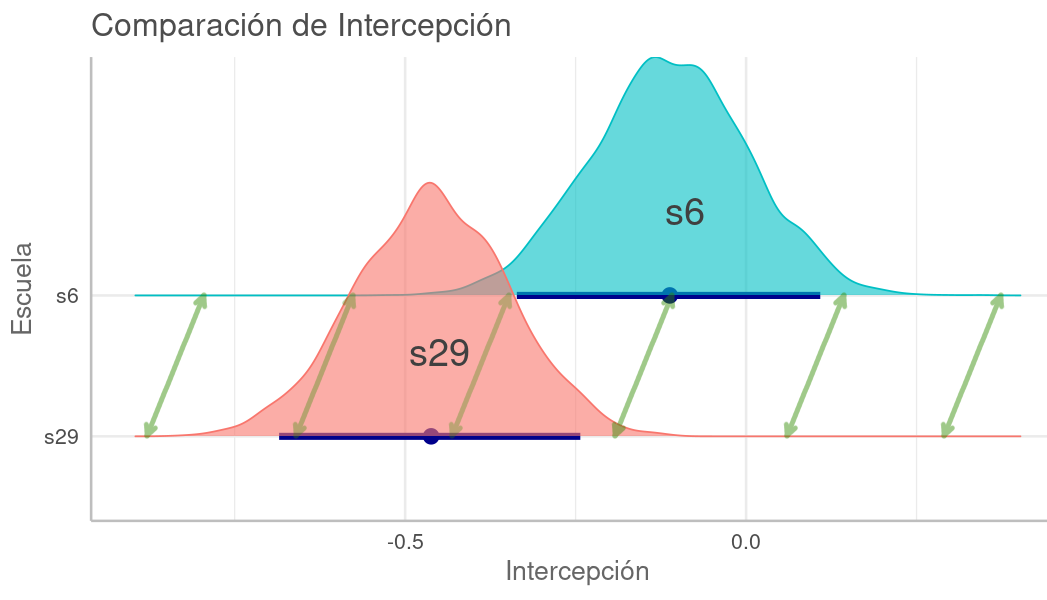
JSP: Comparación de Intercepción de Escuelas s29 y s6. Es contraintuitivo a primera vista del gráfico, pero la Intercepción de la escuela s6 arriba es mayor que el de la escuela s29 abajo en el 99% de las muestras. Se puede tener una intuición de cómo es esto posible si se imagina que cada muestra de la s29 está apareada con una de la s6 como lo sugieren las flechas verdes, donde la mayoría de las muestras de la escuela s6 son mayores que las de la s29.
El gráfico arriba muestra la distribución de la intercepción de dos escuelas, donde en cada base se señala en azul su intervalo creíble al $95\%$ y su media. Como las distribuciones se superponen tanto, a primera vista parece contraintuitivo afirmar que tenemos una certeza del $99\%$ de que la intercepción de la escuela s6 (arriba) es mayor la de la s29 (abajo). Puede tener una intuición de cómo es esto posible si imagina que los valores de las intercepciones están apareadas de la manera como lo sugieren las flechas verdes.
En una inferencia Bayesiana, para comparar dos parámetros, lo hacemos usando sus valores en cada muestra y estimamos la certeza con la proporción de los hallazgos. Por ejemplo, de las $4000$ muestras obtenidas con nuestro modelo, en $3958$ de ellas la intercepción de la escuela s6 es mayor que la de la s29, entonces la probabilidad estimada de esto es $3958/4000=98.95$.
Con brms se pueden probar hipótesis con la función hypothesis(). En nuestro ejemplo anterior la hipótesis es:
hypothesis(jsp_m2,
c("s6>s29" = "r_school[6,Intercept] > r_school[29,Intercept]"),
class = NULL)
Hypothesis Tests for class :
Hypothesis Estimate Est.Error CI.Lower CI.Upper Evid.Ratio Post.Prob Star
1 s6>s29 0.35 0.16 0.1 0.62 94.24 0.99 *
---
'CI': 90%-CI for one-sided and 95%-CI for two-sided hypotheses.
'*': For one-sided hypotheses, the posterior probability exceeds 95%;
for two-sided hypotheses, the value tested against lies outside the 95%-CI.
Posterior probabilities of point hypotheses assume equal prior probabilities.
Donde la columna Estimate muestra el valor estimado de la diferencia entre las intercepciones de las escuelas ($s6-s29$). El valor en Est.Error es la desviación estándar de Estimate. La columna Evid.Ratio es la proporción de la evidencia a favor respecto a la que hay en contra de la hipótesis $Evid.Ratio= 0.9895/(1−0.9895)=94.24$. Finalmente, Post.Prob muestra la proporción de las muestras que están a favor de la hipótesis.
Para entender mejor los resultados de la función hypothesis(), graficamos la distribución de la diferencia de la intercepción de las escuelas (s6 menos s29).
school_diff <- as.data.frame(jsp_m2) %>%
select(`r_school[29,Intercept]`, `r_school[6,Intercept]`) %>%
mutate(intc_29 = `r_school[29,Intercept]`) %>%
mutate(intc_6 = `r_school[6,Intercept]`) %>%
mutate(diff_6_29 = intc_6 - intc_29) %>%
select(intc_29, intc_6, diff_6_29)
s6_greater_prob <- mean(school_diff$diff_6_29 > 0)
diff_sd <- sd(school_diff$diff_6_29)
diff_mean <- mean(school_diff$diff_6_29)
school_diff %>%
ggplot() +
geom_histogram(aes(x = diff_6_29), fill = "lightblue", color = "gray60", alpha = 0.9, bins = 40) +
geom_vline(xintercept = diff_mean, linetype = 2) +
annotate("text", x=diff_mean, y=10,
label=fround(diff_mean)
) +
annotate("text",
x = -0.1, y = 50,
label = (fround(1 - s6_greater_prob) * 100) %cat% "%",
size = 8, color = "red", alpha = 0.6
) +
annotate("text",
x = 0.36, y = 110,
label = (fround(s6_greater_prob, 4) * 100) %cat% "%",
size = 12, color = "blue", alpha = 0.8
) +
annotate("text",
label= "sd=" %cat% fround(diff_sd),
x=0.65, y=230, size=10, color="gray30"
) +
labs(
title = "Diferencia de Intercepción entre Escuelas 6 - 29",
x = "Diferencia de Intercepción 6 - 29",
y = "Cantidad de Muestras"
)
)
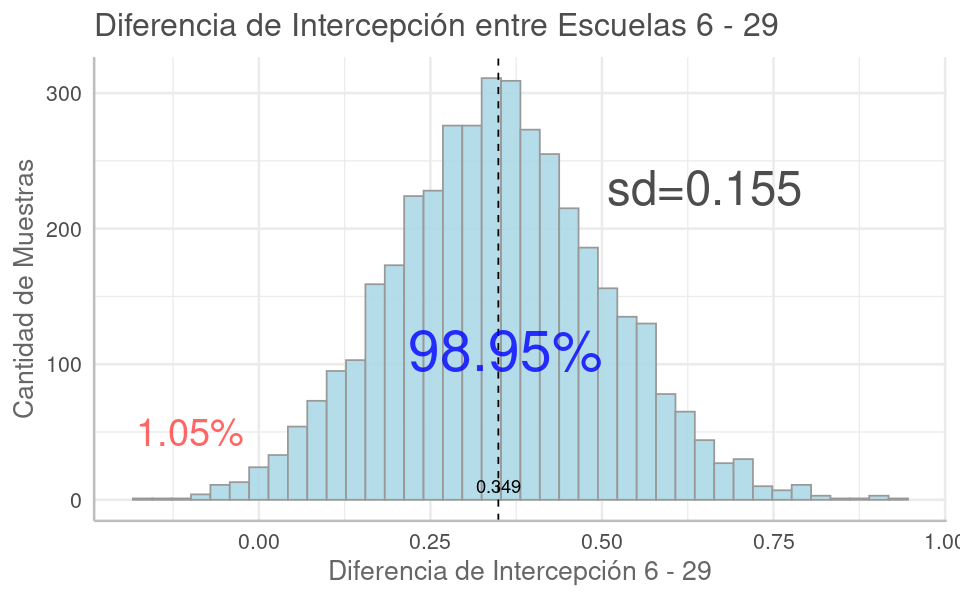
JSP: Diferencia de Intercepciones de Escuelas 6 y 29. En el 98% de las muestras, la Intercepción de la escuela 6 es mayor que el de la 29.
Como esperábamos, el $98.95\%$ de las diferencias es positivo, igual al resultado de hypothesis() en la columna Post.Prob, y su desviación estándar (sd en el gráfico) es igual a Est.Error. La diferencia media es $0.35$, tal como es reportado en la columna Estimate.
Ejemplo comparando la Intercepción por Género
En el listado de nuestro modelo jsp_m2, vemos en la intercepción por género, que las chicas genderf (gender:fem) tienen una muy ligera ventaja (de $0.03-(-0.01)=0.04 \, \sigma_y$) respecto a los chicos genderm (gender:masc). Pero no hay una gran certeza de que ninguna de estas dos intercepciones sea diferente de cero, pues sus intervalos creíbles lo incluyen. ¿Qué podemos decir acerca de la diferencia entre estas dos intercepciones? ¿Tal vez la varianza de la diferencia es tan grande que nos impide afirmar nada acerca de esta diferencia con certidumbre razonable? Resolvamos esto con la ayuda de la función hypothesis().
hypothesis(jsp_m2, "genderf - genderm > 0", class="b")
Hypothesis Tests for class b:
Hypothesis Estimate Est.Error CI.Lower CI.Upper Evid.Ratio Post.Prob Star
1 (genderf-genderm) > 0 0.04 0.03 -0.01 0.09 10.33 0.91
---
'CI': 90%-CI for one-sided and 95%-CI for two-sided hypotheses.
Encontramos que en el $91\%$ de las muestras la diferencia de intercepción es a favor de las chicas.
La alumna promedio de 3er año tiene ligeramente mejor puntaje al 5to que el alumno promedio. Los datos muestran esto con una certidumbre estimada en $91\%$, y la ventaja estimada de las chicas sobre los chicos es de $0.04 \, \sigma_y$.
Efecto de Clase Social del Padre del Alumno
Podemos probar como hipótesis el signo de la intercepción en cada clase social, es decir probar si la clase social del padre tiene un efecto positivo o negativo en el aprendizaje del alumno.
hypothesis(jsp_m2, "Intercept > 0", scope="ranef", group="social")
Hypothesis Tests for class :
Group Hypothesis Estimate Est.Error CI.Lower CI.Upper Evid.Ratio Post.Prob Star
1 I (Intercept) > 0 0.05 0.07 -0.05 0.17 3.45 0.78
2 II (Intercept) > 0 0.06 0.05 -0.02 0.15 7.89 0.89
3 III nonmanual (Intercept) > 0 0.03 0.05 -0.05 0.12 2.54 0.72
4 III manual (Intercept) > 0 -0.03 0.04 -0.10 0.03 0.23 0.19
5 IV (Intercept) > 0 0.00 0.05 -0.09 0.08 0.87 0.47
6 V (Intercept) > 0 -0.07 0.06 -0.18 0.02 0.12 0.11
7 lterm unemp (Intercept) > 0 -0.06 0.06 -0.17 0.03 0.19 0.16
8 curr unemp (Intercept) > 0 -0.02 0.07 -0.14 0.08 0.62 0.38
9 father absent (Intercept) > 0 0.05 0.05 -0.02 0.14 7.53 0.88
Recordemos que en nuestro modelo estas intercepciones son desviaciones alrededor de la media a nivel población. Es decir, están centradas en cero y los valores positivos refieren a intercepciones arriba de la media y viceversa. Es por eso que tiene sentido evaluar la certidumbre que tenemos de estas intercepciones con respecto a cero.
Cuando Evid.Ratio es menor que 1 señala que tenemos más evidencia de que el efecto de social es negativo que positivo. Así, en el caso de la fila $6$, Evid.Ratio=0.12 indica que tenemos $1/0.12=8.3$ veces más evidencia de que el efecto es negativo que positivo, y que correspondientemente la probabilidad de que sea negativa es $1-0.12=88\%$.
La influencia de la clase
socialdel padre en el rendimiento del alumno es pequeña, con una magnitud promedio de $0.04 \, \sigma_y$ y un máximo estimado de $0.07 \, \sigma_y$. Tenemos más certeza de que esta influencia es positiva para alumnos con padres en las dos primeras clases sociales y para la categoríafather absent; y de que es negativa con padres en la última categoríaV, o que estan desempleados a largo plazolterm unemp. Sin embargo, la certidumbre que tenemos de los efectos referidos está en el orden de $[78\% - 89\%]$, hace falta un mayor volumen de datos para mejorar esta certidumbre.Sorprendentemente, la categoría padre ausente
father absenttiene un efecto positivo en el aprendizaje del alumno, con una ventaja de $0.05-(-0.07)=0.12 \, \sigma_y$ cuando es comparado al efecto de un padre en la última categoríaV.
Efecto de la Escuela en el Alumno
Recordemos que con la función ranef() podemos obtener los coeficientes de los predictores por grupo, como la intercepción y el coeficiente de score_3_z por escuela.
ranef(jsp_m2)$school %>% print(digits=3)
, , Intercept
Estimate Est.Error Q2.5 Q97.5
1 -0.326838 0.0838 -0.4910 -0.1671
2 -0.162320 0.1175 -0.4076 0.0626
3 0.102519 0.1365 -0.1658 0.3700
4 0.040418 0.0846 -0.1305 0.2011
5 -0.067128 0.0974 -0.2599 0.1283
6 -0.112183 0.1147 -0.3362 0.1088
:
, , score_3_z
Estimate Est.Error Q2.5 Q97.5
1 0.12259 0.0540 0.01752 0.23031
2 0.05322 0.0664 -0.07661 0.18670
3 -0.03970 0.0776 -0.20149 0.10940
4 -0.01508 0.0529 -0.12086 0.09166
5 0.02551 0.0611 -0.09491 0.14975
6 0.05866 0.0746 -0.07529 0.22207
:
Si consideramos que el 52% de los alumnos en la data son chicas, podemos estimar la intercepción esperada a nivel población con el promedio ponderado de las intercepciones por género y obtener un estimado de $0.0153$. De manera similar, si usamos la distribución de la clase social del padre en la data, con las intercepciones por este grupo, obtenemos $-0.00191$ como intercepción esperada en este concepto, lo que suma $0.0133$. Entonces la intercepción total por escuela es la suma de éste último valor con la intercepción de cada escuela, que como sabemos es el puntaje esperado del alumno promedio en 5to año. Sin embargo, al ser una constante agregada a cada intercepción de escuela, no afecta a la clasificación de estas.
interc_school_m3 <- ranef(jsp_m3)$school %>% as.data.frame()
interc_school_m3$school <- row.names(ranef(jsp_m3)$school)
interc_school_m3 %>%
ggplot(aes(x = school %>% fct_reorder(Estimate.Intercept), y = Estimate.Intercept)) +
geom_point(color = "dodgerblue") +
geom_hline(yintercept = 0, color = "gray70", linetype = 2) +
geom_errorbar(aes(ymin = Q2.5.Intercept, ymax = Q97.5.Intercept), color = "darkblue") +
coord_cartesian(ylim = c(-0.8, 0.8)) +
labs(
title = "JSP: Intercepciones por Escuela", subtitle = "Intervalos al 95%",
x = "Id de Escuela", y = "Intercepción Estimada (95%)"
) +
x_text_45
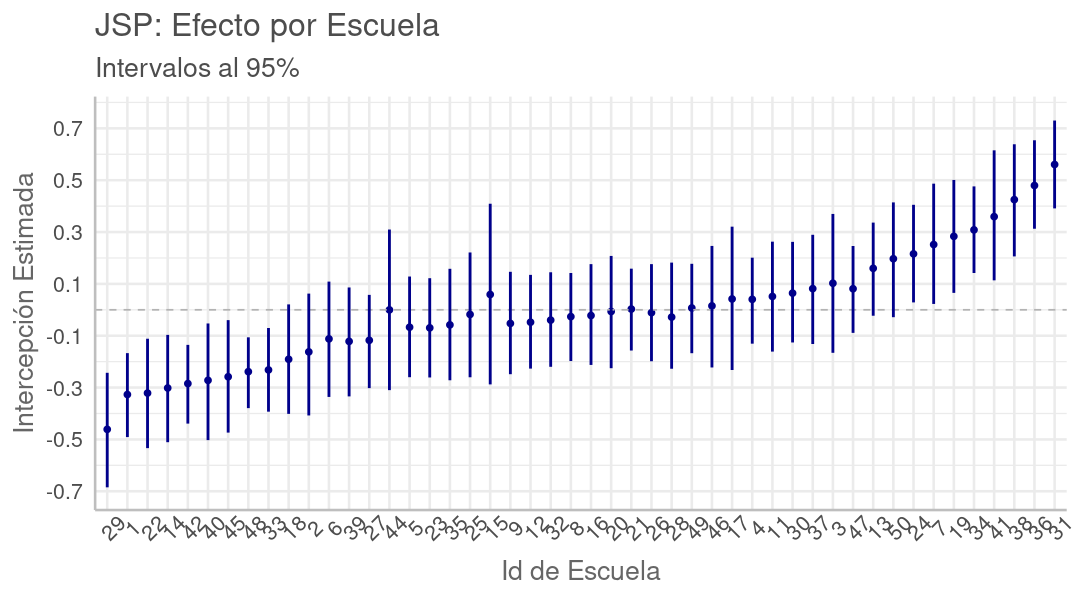
JSP: Intercepciones por Escuela. El punto representa la Intercepción estimada y las barras verticales su intervalo de variación al 95%. Las escuelas están ordenadas a lo largo del eje horizontal aproximadamente por la intercepción estimada.
Si con las proporciones en la data, estimamos los coeficientes para la escuela con menor intercepción, tenemos:
$$\begin{aligned} \text{Escuela con menor intercepción:} \\ \text{score_5_z} &= (0.01529 - 0.00191) + (0.1681 + 0.00437) \, \text{raven_z} \\ &+ 0.6167 \, \text{score_3_z} + (-0.4611 + 0.1556 \, \text{score_3_z} ) \\ &= 0.01338 + 0.1725 \, \text{raven_z} + 0.6167 \, \text{score_3_z} \\ &+ (-0.4611 + 0.1556 \, \text{score_3_z} ) \\ &= −0.4477 + 0.1725 \, \text{raven_z} + 0.7723 \, \text{score_3_z} \end{aligned}$$
Donde $0.01529$ es la intercepción ponderada por gender, $-0.00191$ es la intercepción ponderada por social, $+0.00437$ es la pendiente de raven_z ponderada por social, y el último término entre paréntesis son los coeficientes de la escuela con menor intercepción; los demás son coeficientes a nivel población. Procediendo de la misma manera con la escuela con mayor intercepción:
$$\begin{aligned} \text{Escuela con mayor intercepción:} \\ \text{score_5_z} &= 0.01338 + 0.1725 \, \text{raven_z} + 0.6167 \, \text{score_3_z} \\ & + (0.5606 -0.1887 \, \text{score_3_z} ) \\ &= 0.5740 + 0.1725 \, \text{raven_z} + 0.4280 \, \text{score_3_z} \end{aligned}$$
Donde un alumno promedio en la mejor escuela tiene un puntaje $0.5740 - (-0,4477)=1.02 \, \sigma_y$ mayor que uno en la peor. Para que el alumno de la peor escuela pueda alcanzar al de la mejor, se requiere que:
$$\begin{aligned} 0.5740 &= −0,4477 + 0.1725 \, \text{raven_z} + 0.7723 \, \text{score_3_z} \\ 1.02 &= 0.1725 \, \text{raven_z} + 0.7723 \, \text{score_3_z} \end{aligned}$$
Donde una solución posible es $\text{raven_z} = 1.08$ y $\text{score_3_z}=1.08$, pues $0.1725 \times 1.08 + 0.7723 \times 1.08 = 1.02 \, \sigma_y$
La escuela tiene un gran impacto en el aprendizaje del alumno. El efecto de la escuela con mayor influencia positiva comparada con la de mayor influencia negativa en el aprendizaje del alumno tiene una ventaja estimada en $1.02$ desviaciones estándar en el puntaje obtenido por el alumno promedio al 5to año.
Para que un alumno en la escuela con mayor influencia negativa pueda alcanzar al alumno promedio en la escuela con mayor influencia positiva, requiere que tenga puntajes en 3er año y de razonamiento abstracto con una desviación estándar por encima del promedio de la población.
Clasificación de las Escuelas
Vamos a hacer una comparación cruzada de la intercepción de cada escuela contra todas las demás ($49 \times (49-1)/2=1176$ comparaciones) usando la prueba de hipótesis que vimos anteriormente. En cada comparación concluiremos que una escuela tiene mayor efecto positivo —sobre el alumno— que otra, cuando la certeza sea mayor o igual al $95\%$. El clasificar a las escuelas por intercepción, equivale a hacerlo según su efecto sobre el alumno promedio.
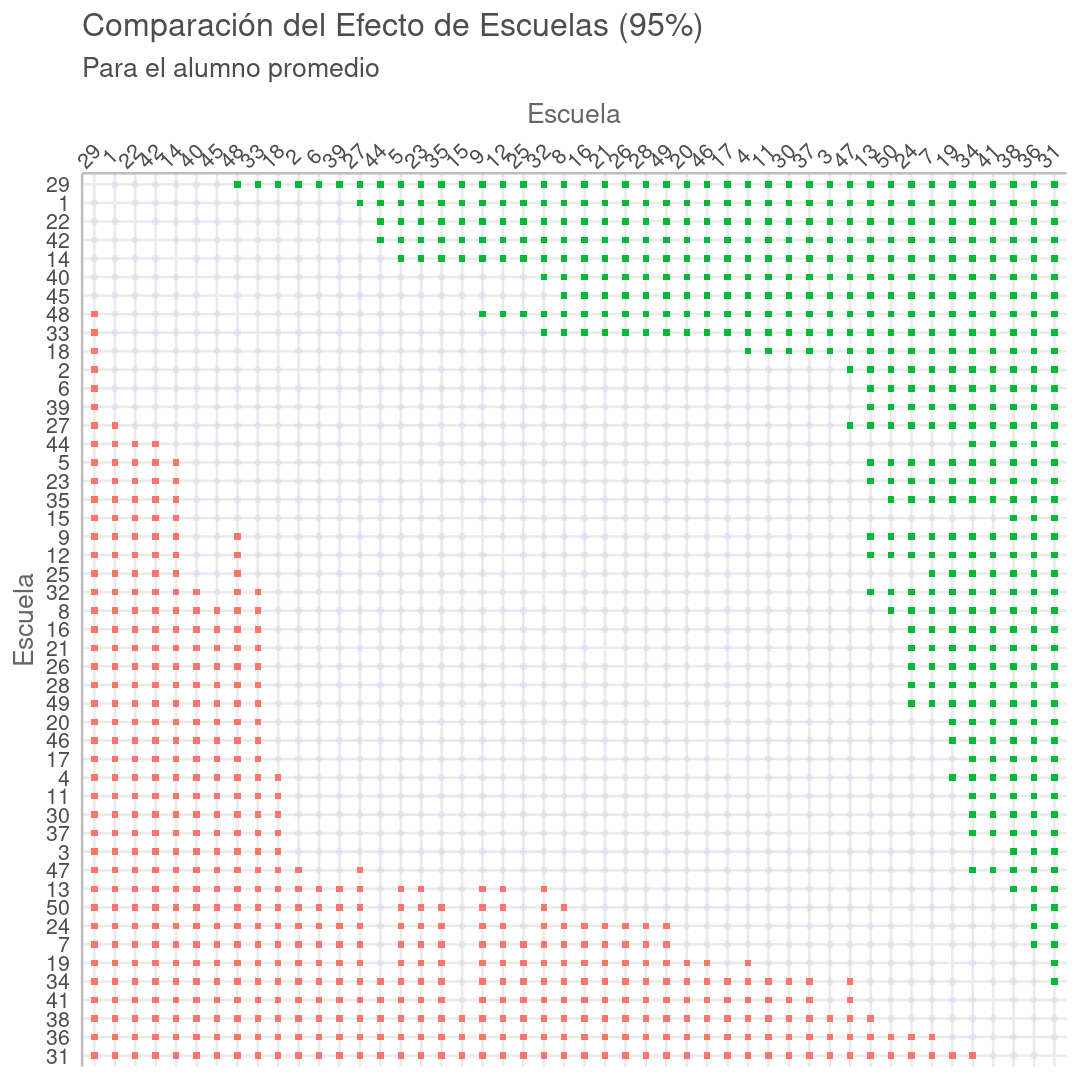
JSP: Comparación de cada escuela contra todas las demás. Cada punto verde señala que la escuela en la fila tiene mayor efecto (95% o más) que la escuela en la columna. Cada punto rojo señala lo opuesto, también al 95%.
En el gráfico arriba, cada punto de color verde señala que la escuela en el eje horizontal tiene un efecto positivo mayor sobre el alumno promedio que la escuela en el eje vertical, con una certidumbre mayor o igual que $95\%$. Por ejemplo, la escuela 27 tiene un efecto mayor que las escuelas 29 y 1. Los puntos de color rojo señalan lo opuesto, así la 7 tiene un efecto menor que las escuelas 36, y 31.
La zona intermedia, sin puntos, contiene las combinaciones de escuelas para las que no hay certidumbre (al 95%) de cuál es mejor que la otra. Para poder resolver mejor estos casos se necesita un volumen mayor de datos. Sin embargo, hemos podido discriminar en $1042$ de $2352$ comparaciones, el $44\%$ de todas ellas, que es algo que no podríamos hacer con solo los intervalos mostrados en el gráfico "JSP: Intercepciones por Escuela" como ocurre en regresiones con estimaciones puntuales.
Referencias
[Burkner] P. Burkner PC (2017). “brms: An R Package for Bayesian Multilevel Models using Stan.” Journal of Statistical Software, 80(1), 1–28. doi:10.18637/jss.v080.i01.
[Gelman] Andrew Gelman, 2006. Prior distributions for variance parameters in hierarchical models. http://www.stat.columbia.edu/~gelman/research/published/taumain.pdf.
[Gelman] Andrew Gelman, Jennifer Hill, Masanao Yajima. "Why We (Usually) Don’t Have to Worry About Multiple Comparisons", 2013. Journal of Research on Educational Effectiveness. http://www.stat.columbia.edu/~gelman/research/published/multiple2f.pdf
[Gelman] Andrew Gelman, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press.
[Gustafson] Paul Gustafson, Shahadut Hossain, and Ying C. MacNab. 2006.Conservative Prior Distributions for Variance Parameters in Hierarchical Models. The Canadian Journal of Statistics. https://doi.org/10.1002/cjs.5550340302.
[Goldstein] Goldstein, H. (1995). "Multilevel Statistical Models". London, Edward Arnold.
[Joox] Joop J. Hox. 2010. Multilevel Analysis Techniques and Applications, Second Edition. Routledge
[Lai et al. 2015] Lai, Mark H. C., and Oi-man Kwok. 2015. “Examining the Rule of Thumb of Not Using Multilevel Modeling: The ‘Design Effect Smaller Than Two’ Rule.” The Journal of Experimental Education 83: 423–38. https://doi.org/10.1080/00220973.2014.907229.
[LKJ] Lewandowski, Daniel; Dorota Kurowicka; and Harry Joe. 2009. “Generating Random Correlation Matrices Based on Vines and Extended Onion Method.” Journal of Multivariate Analysis 100: 1989–2001.
[McElreath] Richard McElreath. 2018. "Statistical Rethinking: A Bayesian Course with Examples in R and Stan". CRC Press.
[Mortimer] Peter Mortimer et al. "A study of effective junior schools", 1989. International Journal of Educational Research. https://www.academia.edu/24104539/A_study_of_effective_junior_schools.
[stan] Carpenter B.; Gelman A.; Hoffman M. D.; Lee D.; Goodrich B.; Betancourt M.; Brubaker M.; Guo J.; Li P.; and Riddell A. 2017. "Stan: A probabilistic programming language". Journal of Statistical Software. 76(1). 10.18637/jss.v076.i01
Anexos
Generación de Datos Simulados Toy
El código con el que se ha generado la data es:
make_data <- function() {
beta <- c(b0 = 2.7, b1 = 1.3)
sigma_y <- 1.6
mu_alpha <- c(a0 = 6.2, a1 = 2.3)
sigma_alpha <- c(a0 = 1.4, a1 = 0.9)
rho <- 0.4
cov_alpha <- rho * sigma_alpha["a0"] * sigma_alpha["a1"]
J <- 48
mu_n_j <- 20
sigma_n_j <- 3
min_x <- 0
max_x <- 6
Sigma_alpha <- matrix(c(sigma_alpha["a0"]^2, cov_alpha, cov_alpha, sigma_alpha["a1"]^2), 2, 2)
data <- data.frame(x = numeric(), y = numeric(), g = character())
coefs <- data.frame(intercept=numeric(), slope=numeric())
set.seed(123)
for (j in 1:J) {
n_j <- sample(2:21, size=1, replace = T, prob=seq(15,10,length.out = 20))
alpha_j <- MASS::mvrnorm(n = 1, mu = mu_alpha, Sigma = Sigma_alpha)
names(alpha_j) <- c("a0", "a1")
intercept <- beta["b0"] + alpha_j["a0"]
slope <- beta["b1"] + alpha_j["a1"]
coefs <- coefs %>% bind_rows(data.frame(intercept=intercept, slope=slope, g=as.character(j)))
for (i in 1:n_j) {
x <- runif(n=1, min = min_x, max = max_x)
y <- rnorm(n = 1, mean = intercept + slope * x, sd = sigma_y)
data <- data %>% bind_rows(data.frame(x=x, y=y, g=as.character(j)))
}
}
row.names(coefs) <- NULL
return(list(data, coefs))
}
data_list <- make_data()
data <- data_list?span><span class="hl opt">
true_coefs <- data_list?span><span class="hl opt">
data <- data %>% add_row(x=data$x[73], y=data$y[73], g="49")
data$g <- factor(data$g, levels=as.character(1:49))
true_coefs <- true_coefs %>%
add_row(intercept=true_coefs$intercept[6], slope=true_coefs$slope[6], g="49") %>%
mutate(g = factor(true_coefs$g, levels=as.character(1:49)))